山东省威海市文登区2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 下列图形,一定是轴对称图形的是( )A、直角三角形 B、梯形 C、平行四边形 D、线段2. 以下列各组数为边长的三角形中,能够构成直角三角形的是( )A、32 , 42 , 52; B、2, , ; C、 ; D、 , ,3. 若点 在第二象限,则点 在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 等腰三角形的两边长是6cm和3cm,那么它的周长是A、9cm B、12 cm C、12 cm或15 cm D、15 cm5. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )

A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD6. 平面直角坐标系中,一个图案上各个点的横坐标都乘以 ,纵坐标不变,得到一个图案,下列结论正确的是( )A、新图案是原图案向下平移了 个单位 B、新图案是原图案向左平移了 个单位 C、新图案与原图案关于x轴对称 D、新图案与原图案形状和大小完全相同7. 下列说法中正确的是( )A、 的平方根是 B、 的算术平方根是 C、 与 相等 D、 的立方根是8. 如图,在 中, , 于点D, 平分 交 于点E,则下列结论一定成立的是( ) A、 B、 C、 D、9. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A、 B、 C、 D、9. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A、7.5平方千米 B、15平方千米 C、75平方千米 D、750平方千米10. 把直线 向上平移 个单位长度,再向左平移 个单位长度,得到的直线的表达式为( )A、 B、 C、 D、11. 七巧板是大家熟悉的一种益智类玩具.用七巧板能拼出许多有趣的图案.小明将一个直角边长为 的等腰直角三角形纸板,切割七块.正好制成一副七巧板,则图中阴影部分的面积为( ) A、 B、 C、 D、12. 如图, ,点D,E在 边上,点F在 边上.将 沿 折叠,恰好与 重合,将 沿 折叠,恰好与 重合.下列结论:
A、 B、 C、 D、12. 如图, ,点D,E在 边上,点F在 边上.将 沿 折叠,恰好与 重合,将 沿 折叠,恰好与 重合.下列结论:① ② ③ ④ ⑤
正确的个数有( )
 A、 个 B、 个 C、 个 D、 个
A、 个 B、 个 C、 个 D、 个二、填空题
-
13. 在实数① ② ③ ④ 中,无理数有 . (只填写序号)14. 若正比例函数 的函数值y随x的增大而增大,且函数图象上的点到两坐标轴的距离相等,则m的值为 .15. 如图, 中, , 是 的垂直平分线,交 于点E,交 于点D.连接 .若 , ,则 的周长为 .
 16. 为等边三角形,点D为 边上一点,以 为边做等边三角形 ,使点E,A在直线 的同侧,连接 ,则 的度数为 .
16. 为等边三角形,点D为 边上一点,以 为边做等边三角形 ,使点E,A在直线 的同侧,连接 ,则 的度数为 .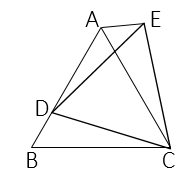 17. “赵爽弦图”巧妙的利用面积证明了勾股定理.如图所示的“赵爽弦图”是用四个全等的直角三角形和一个小正方形拼成一个大正方形.若直角三角形两直角边分别为 , ,且 ,大正方形的面积为 ,则 .
17. “赵爽弦图”巧妙的利用面积证明了勾股定理.如图所示的“赵爽弦图”是用四个全等的直角三角形和一个小正方形拼成一个大正方形.若直角三角形两直角边分别为 , ,且 ,大正方形的面积为 ,则 .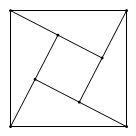 18. 如图, , 在射线 上, .取 的中点 ,以 为腰, 为顶角作等腰三角形 ;取 的中点 ,以 为腰, 为顶角作等腰三角形 ;取 的中点 ,以 为腰, 为顶角作等腰三角形 ,若 ,则 的度数为 .
18. 如图, , 在射线 上, .取 的中点 ,以 为腰, 为顶角作等腰三角形 ;取 的中点 ,以 为腰, 为顶角作等腰三角形 ;取 的中点 ,以 为腰, 为顶角作等腰三角形 ,若 ,则 的度数为 .
三、解答题
-
19. 计算:(1)、 ;(2)、已知 ,求 的立方根;(3)、如图,一次函数 的图像分别与x轴、y轴交于点A、B,且经过点 ,求 的面积.
 20. 如图,C,D是线段 上两点, 于点D, 于点C.连接 , .若 , .求证: .
20. 如图,C,D是线段 上两点, 于点D, 于点C.连接 , .若 , .求证: .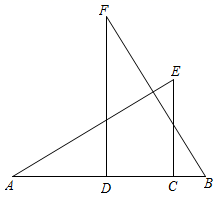 21. 已知线段a,利用尺规作四边形 ,使 .(保留作图痕迹,不写作法)
21. 已知线段a,利用尺规作四边形 ,使 .(保留作图痕迹,不写作法) 22. 如图,将长方形 沿对角线 折叠,使点C落在E处, 交 于点F.
22. 如图,将长方形 沿对角线 折叠,使点C落在E处, 交 于点F. (1)、判断 的形状,并说明理由;(2)、若 , ,求 的面积.23. 本学期第四章《实数》中,我们学习了平方根和立方根,下表是平方根和立方根的部分内容:
(1)、判断 的形状,并说明理由;(2)、若 , ,求 的面积.23. 本学期第四章《实数》中,我们学习了平方根和立方根,下表是平方根和立方根的部分内容:平方根
立方根
定义
一般地,如果一个数x的平方等于a,即 ,那么这个数x就叫做a的平方根(也叫做二次方根).
一般地,如果一个数x的立方等于a,即 ,那么这个数x就叫做a的立方根(也叫做三次方根).
运算
求一个数a的平方根的运算叫做开平方.开平方和平方互为逆运算.
求一个数a的立方根的运算叫做开立方.开立方和立方互为逆运算
性质
一个正数有两个平方根,它们互为相反数:0的平方根是0;负数没有平方根.
正数的立方根是正数;0的立方根是0;负数的立方根是负数.
表示方法
正数a的平方根可以表示为“ ”
一个数a的立方根可以表示为“ ”
今天我们类比平方根和立方根的学习方法学习四次方根.
(类比探索)
(1)、探索定义:填写下表类比平方根和立方根,给四次方根下定义:
.
(2)、探究性质:① 的四次方根是;② 的四次方根是;
③ 的四次方根是;④ 的四次方根是;
⑤ 的四次方根是;⑥ (填“有"或"“没有”)四次方根.
类比平方根和立方根的性质,归纳四次方根的性质:
;
(3)、在探索过程中,你用到了哪些数学思想?请写出两个: .(拓展应用)
① ;
② ;
③比较大小: .
24. 甲、乙两车分别从A,B两地同时出发,甲车匀速前往B地,到达B地后以另一速度返回A地;乙车匀速前往A地.甲、乙两车距A地的路程y(千米)与行驶时间t(小时)的关系如图所示. (1)、求甲车到达B所用的时间;(2)、求乙车距A地的路程y(千米)与时间t(小时)的函数表达式;(3)、求乙车到达A地时,甲车与A地之间的距离.25.(1)、(问题情境)
(1)、求甲车到达B所用的时间;(2)、求乙车距A地的路程y(千米)与时间t(小时)的函数表达式;(3)、求乙车到达A地时,甲车与A地之间的距离.25.(1)、(问题情境)如图 ,在四边形 中, , , .点E,F分别是 和 上的点,且 ,试探究线段 , , 之间的关系.小明同学探究此问题的方法是:延长 到点G,使 ,连接 .先证明 ,再证明 ,进而得出 .你认为他的做法;(填“正确”或“错误”).
 (2)、(探索延伸)
(2)、(探索延伸)如图 ,在四边形 中, , , , ,点E,F分别是 和 上的点,且 ,上题中的结论依然成立吗?请说明理由.
 (3)、(思维提升)
(3)、(思维提升)小明通过对前面两题的认真思考后得出:如图 ,在四边形 中,若 , , ,那么 .你认为符合题意吗?请说明理由.
