山东省青岛市市北区2020-2021学年七年级上学期数学期末试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列调查中、宜采用抽样调查的是（）

A、了解某班全体学生的身高情况 B、某企业招聘，了解所有的应聘人员基本信息 C、乘飞机前对乘客进行安全检查 D、调查某城市全体市民的月均用水量

查看试题解析
2. 南海是我国最大的领海，总面积有3500000 $k m^{2}$ ，3500000用科学记数法可表示为（）

A、3.5×10 $^{4}$ B、3.5×10 $^{5}$ C、3.5×10 $^{6}$ D、0.35×10 $^{7}$

查看试题解析
3. 如图，数轴上A、B、C、D四个点中，表示的数互为相反数的是（）

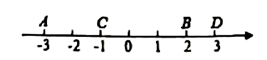A、点A与点B B、点C与点B C、点A与点D D、点C与点D

查看试题解析
4. 下列四个几何体，从正面和上面看所得到的视图都为长方形的是（）

A、 B、 C、 D、

查看试题解析
5. 若x＝|﹣3|，|y|＝2，则x+2y的值为（）

A、﹣7 B、﹣1 C、﹣7或1 D、7或﹣1

查看试题解析
6. 已知一个直角三角形的两条直角边长分别是：3cm和4cm，以其中一条直角边所在直线为轴旋转一周，得到的几何体的底面积是（）

A、 $4 π c m^{2}$ B、 $9 π c m^{2}$ C、 $2.25 π c m^{2}$ 或 $4 π c m^{2}$ D、 $9 π c m^{2}$ 或 $16 π c m^{2}$

查看试题解析
7. 某村原有林地108公顷，旱地54公顷，为保护环境，需把一部分旱地改造为林地，使旱地占林地面积的20%，设把x公顷旱地改为林地，则可列方程（）

A、54−x=20%×108 B、54−x=20%×（108+x） C、54+x=20%×162 D、108−x=20%（54+x）

查看试题解析
8. 如图所示，将正整数1至2020按一定规律排列成数表，平移表中带阴影的方框，方框中三个数的和可能是（）

A、2018 B、2019 C、2013 D、2040

查看试题解析

二、填空题

9. 小明向东走100米，记作＋100米，那么向西走20米记作米．

查看试题解析
10. 1.45°=′．

查看试题解析
11. 一个直棱柱有21条棱，那么这个棱柱的底面的形状是．

查看试题解析
12. 如图是一，二两组同学将本组最近 $5$ 次数学平均成绩．分别绘制成的折线统计图．由统计图可知组进步更大．(选填“一"或"二”)

查看试题解析
13. 点O，A，B，C在数轴上的位置如图所示．O为原点，AC＝1，OA＝OB，若点C所表示的数为a，则点B表示的数为．

查看试题解析
14. 如果八折购买一本书，比九折购买少2元，那么这本书的原价是元．

查看试题解析
15. 如图：把一张边长为15cm的正方形硬纸板的四个角各剪去一个同样大小的正方形，再折成一个无盖的长方体盒子（纸板的厚度忽略不计），当剪去的正方形边长从4cm变为6cm后，长方体纸盒容积变（填大或小）了 $c m^{2}$ ．

查看试题解析
16. 观察下列由长为1，的小正方体摆成的图形，如图①所示共有1.个小立方体，其中1个看得见，0个看不见：如图②所示：共有8.个小立方体，其中7个看得见，1个看不见：如图③所示：共有27个小立方体，其中19个看得见，8个看不见…按照此规律继续摆放：

(1)、第④个图中，看不见的小立方体有个：

(2)、第n个图中，看不见的小立方体有个．

查看试题解析

三、解答题

17. 已知：线段a，b（如图），画出线段AB，使AB＝a－2b。（用尺规作图，不写作法，保留作图痕迹）

查看试题解析
18. 计算

(1)、 $(- \frac{3}{4} - \frac{7}{12} - \frac{5}{8}) \times (- 24)$

(2)、 $- 2^{2} + | 3 - 8 | - 24 \div (- 5) \times \frac{1}{5}$

查看试题解析
19.

(1)、已知：a．b满足 $7.76 \times 10^{4}$ ，求：单项式 $- 5 a x^{a - b} y$ 的系数和次数分别是什么？

(2)、化简求值： $3 (- \frac{2}{3} a + \frac{1}{3} b^{2}) - \frac{1}{2} (6 a^{2} - b^{2})$ ．其中 $a = - 2 ， b = 1$ ．

查看试题解析
20. 解方程：

(1)、 $3 x - 2 = 1 - 2 (x + 1)$

(2)、 $\frac{2 x + 1}{3} - \frac{5 x - 1}{6} = 1$

查看试题解析
21. 某校体育节决定开设A：乒乓球，B：篮球，C：跑步，D：跳绳，这四种运动项目的竞事，为了解学生喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如图所示的条形统计图和扇形统计图，请你结合图中的信息解答下列问题

(1)、列式计算本次调查共抽取学生的人数：

(2)、把条形统计图补充完整：

(3)、列式计算扇形统计图中B所对的圆心角的度数．

查看试题解析
22. 如图已知点C为AB上一点，AC＝12cm， CB＝ $\frac{2}{3}$ AC，D、E分别为AC、AB的中点．求DE的长．

查看试题解析
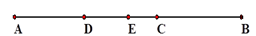23. 列方程解应用题：某车间原计划13小时生产一批零件，技术革新提升了产能，实际每小时多生产10件，用12小时不仅完成任务，而且还较原计划多生产了60件．求：原计划每小时生产的零件数．

查看试题解析
24. 已知：如图，点O在直线AC上，OD平分∠AOB， $∠ B O E = \frac{1}{2} ∠ E O C ， ∠ D O E = 70^{\circ}$ ，求：∠EOC的度数．

查看试题解析
25. 我市某医药公司要把药品运往外地，现有两种运输方式可供选择：
方式一：使用快递公司的邮车运输，装卸收费400元，每公里运费4元：

方式二：使用铁路运输公司的火车运输，装卸收费820元，每公里运费2元．

(1)、若运物路程为x公里，请你用代数式分别表示这两种运输方式的收费：

(2)、运输路程是多少公里时，这两种方式的收费相同？

(3)、如果这批药品准备运往距离300公里远的目的地，忽略其他因素的影响，你认为选用哪种运输方式更合算？通过计算说明理由．

查看试题解析