江西省赣州市大余县2020-2021学年七年级上学期数学期末试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. -2021的倒数是( )A、 B、 C、2021 D、-20212. 下列计算正确的是( )A、3a+2a=5a2 B、﹣2ab+2ab=0 C、2a3+3a2=5a5 D、3a﹣a=33. 2020年6月23日,北斗三号最后一颗全球组网卫星从西昌卫星发射中心发射升空,6月30 成功定点于距离地球36 000公里的地球同步轨道.将36 000用科学记数法表示应为( )A、0.36×105 B、3.6×105 C、3.6×104 D、36×1034. 如图,已知∠AOC=∠BOD=90°,AOD=120°,∠BOC的度数为( )
 A、60° B、50° C、45° D、30°5. 如图所示,正方体的展开图为( )
A、60° B、50° C、45° D、30°5. 如图所示,正方体的展开图为( ) A、
A、 B、
B、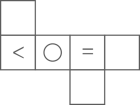 C、
C、 D、
D、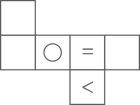 6. 《九章算术》是中国古代的数学专著,奠定了中国传统数学的基本框架.方程术是《九章算术》最高的数学成就. 《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”译文:“假设有若干人共同出钱买羊,如果每人出5钱,那么还差45钱;如果每人出7钱,那么仍旧差3钱,求买羊的人数和羊的价钱.”设羊是x钱,可列方程为( )A、 B、 C、 D、
6. 《九章算术》是中国古代的数学专著,奠定了中国传统数学的基本框架.方程术是《九章算术》最高的数学成就. 《九章算术》中记载:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”译文:“假设有若干人共同出钱买羊,如果每人出5钱,那么还差45钱;如果每人出7钱,那么仍旧差3钱,求买羊的人数和羊的价钱.”设羊是x钱,可列方程为( )A、 B、 C、 D、二、填空题
-
7. 已知一个角的度数为58°,则它的余角的度数是 .8. 若代数式x2+3x﹣5的值为2,则代数式2x2+6x﹣3的值为 .9. 如图,C是线段AB上一点,D是AC的中点,如果AB=10cm,CB=4cm.则AD的长为cm
 10. 若x、y为有理数,且 ,则 的值为 .11. 填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值应是 .
10. 若x、y为有理数,且 ,则 的值为 .11. 填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值应是 . 12. 若A、B、P是数轴上三点,且点A表示的数为﹣1,点B表示的数为3,点P表示的数为x , 当其中一点到另外两点的距离相等时,则x的值可以是
12. 若A、B、P是数轴上三点,且点A表示的数为﹣1,点B表示的数为3,点P表示的数为x , 当其中一点到另外两点的距离相等时,则x的值可以是三、解答题
-
13.(1)、计算:﹣12+5-15+25;(2)、化简:2(2a-b)-3(a+b)14. 把下列各数在数轴上表示出来,并按从小到大的顺序用“ ”连接起来.
 15. 补全下面的解题过程:
15. 补全下面的解题过程:如图,已知OC是∠AOB内部的一条射线,OD是∠AOB的平分线,∠AOC=2∠BOC且∠BOC=40°,求∠COD的度数.

解:因为∠AOC=2∠BOC,∠BOC=40°,
所以∠AOC= ▲ °,
所以∠AOB=∠AOC+∠ ▲ =120°.
因为OD平分∠AOB,
所以∠AOD= ∠ ▲ = ▲ °,
所以∠COD=∠ ▲ ﹣∠AOD= ▲ °.
16. 先化简,再求值:﹣a2b+(3ab2﹣a2b)﹣2(2ab2﹣a2b),其中a=1,b=﹣2.17. 如图是由4个大小相同的正方体组合而成的几何体,请你按下列要求画出平面图形. 18. 赣州享有“世界橙乡”的美誉,中华名果赣南脐橙热销世界各地.刚大学毕业的小明把自家的脐橙产品放到了网上售卖,他原计划每天卖100kg脐橙,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负.单位:kg).
18. 赣州享有“世界橙乡”的美誉,中华名果赣南脐橙热销世界各地.刚大学毕业的小明把自家的脐橙产品放到了网上售卖,他原计划每天卖100kg脐橙,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况(超额记为正,不足记为负.单位:kg).星期
一
二
三
四
五
六
日
与计划量的差值
(1)、根据记录的数据可知前三天共卖出kg;(2)、根据记录的数据可知销售量最多的一天比销售量最少的一天多销售kg;(3)、若脐橙按4.5元/kg出售,且小明需为买家支付运费(平均0.5元/kg),则小明本周一共赚了多少元?19. 对于任意四个有理数a,b,c,d,可以组成两个有理数对(a,b)与(c,d).我们规定:(a,b)★(c,d)=bc-ad.例如:(1,2)★(3,4)=2×3-1×4=2.
根据上述规定解决下列问题:
(1)、有理数对(2,-3)★(3,-2)=;(2)、若有理数对(-3,2x-1)★(1,x+1)=7,求x的值;20. 已知多项式 是六次多项式,单项式3x2ny5-m的次数也是六,求:(1)、m , n的值;(2)、 的值.21. 情景:试根据图中信息,解答下列问题: (1)、购买8根跳绳需元,购买14根跳绳需元.(2)、小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.22. 已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.(1)、计算B的表达式;(2)、求出2A﹣B的结果;(3)、小强同学说(2)中的结果的大小与c的取值无关,对吗?若a= ,b= ,
(1)、购买8根跳绳需元,购买14根跳绳需元.(2)、小红比小明多买2根,付款时小红反而比小明少5元,你认为有这种可能吗?若有,请求出小红购买跳绳的根数;若没有,请说明理由.22. 已知A=3a2b﹣2ab2+abc,小明同学错将“2A﹣B“看成”2A+B“,算得结果为4a2b﹣3ab2+4abc.(1)、计算B的表达式;(2)、求出2A﹣B的结果;(3)、小强同学说(2)中的结果的大小与c的取值无关,对吗?若a= ,b= ,求(2)中式子的值.
23. 综合与实践问题情境
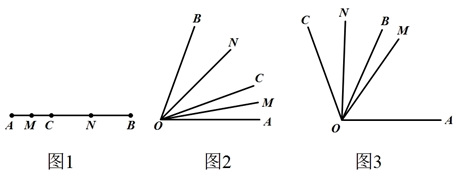
在数学活动课上,老师和同学们以“线段与角的共性”为主题开展数学活动,发现线段的中点的概念与角的平分线的概念类似,甚至它们在计算的方法上也有类似之处,它们之间的题目可以转换,解法可以互相借鉴.如图1,点C是线段AB上的一点,M是AC的中点,N是BC的中点.
 (1)、问题探究
(1)、问题探究①若AB=6,AC=2,求MN的长度.(写出计算过程)
②若AB=a , AC=b , 则MN= ▲ . (直接写出结果)
(2)、继续探究“创新”小组的同学类比想到:如图2,已知∠AOB=70°,在角的内部作射线OC , 再分别作∠AOC和∠BOC的角平分线OM , ON .
③若∠AOC=20°,求∠MON的度数.(写出计算过程)
④若∠AOC=m , 则∠MON= ▲ . (直接写出结果)
(3)、深入探究“慎密”小组在“创新”小组的基础上提出:如图3,若∠AOB=n , 在角的外部作射线OC , 再分别作∠AOC和∠BOC的角平分线OM , ON , 若∠AOC=m , 则∠MON= . (直接写出结果)