初中数学湘教版八年级下册第四单元 一次函数 单元练习

试卷更新日期：2021-04-19 类型：单元试卷

进入 出卷网 下载

一、单选题

  • 1. 下列各种图象中，y不是x的函数的是（    ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 函数 y=x3−x 中自变量 x 的取值范围是（  ）
    A、x>0 B、x≠3 C、x>o且x≠3 D、x≥0且x≠3

    查看试题解析

  • 3. 直线 y=3−2x 不经过的象限是 （    ）
    A、第四象限 B、第三象限 C、第二象限 D、第一象限

    查看试题解析

  • 4. 把直线y=2x﹣1向左平移1个单位，平移后直线的关系式为（  ）
    A、y=2x﹣2 B、y=2x+1 C、y=2x D、y=2x+2

    查看试题解析

  • 5. 正比例函数y=kx（k≠0）和一次函数y=k（1﹣x）在同一个直角坐标系内的图象大致是下图中的（   ）
    A、 B、 C、 D、

    查看试题解析

  • 6. 已知一次函数 y=(k−1)x . 若 y 随 x 的增大而增大，则 k 的取值范围是（   ）
    A、k<1 B、k>1 C、 D、

    查看试题解析

  • 7. 正比例函数y=kx（k≠0）的图象经过第二、四象限，则一次函数y=x+k的图象大致是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 8. 已知点（﹣2，y1），（﹣1，y2），（1，y3）都在直线y=4x+2上，则y1 ， y2 ， y3的值的大小关系是（   ）
    A、y3＜y1＜y2 B、y1＜y2＜y3 C、y3＞y1＞y2 D、y1＞y2＞y3

    查看试题解析

  • 9.

    如图，在矩形ABCD中，AB=2，AD=3，点E是BC边上靠近点B的三等分点，动点P从点A出发，沿路径A→D→C→E运动，则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是（   ）

    A、 B、 C、 D、

    查看试题解析

  • 10. 如图，直线y=-x+4分别与x轴，y轴交于A，B两点．从点P(2，0)射出的光线经直线AB反射后又经直线OB反射回到P点，则光线第一次的反射点Q的坐标是（  ）

    A、(2，2) B、(2.5，1.5) C、(3，1)  D、(1.5，2.5)

    查看试题解析

二、填空题

  • 11. 若函数y=（a-3）x|a|-2+2a+1是一次函数，则a=.

    查看试题解析

  • 12. 如图，该直线是某个一次函数的图象，则此函数的解析式为.

    查看试题解析

  • 13. 按如图所示的运算程序，输入一个有理数x，便可输出一个相应的有理数y，写出y与x之间的关系式： ．

    查看试题解析

  • 14. 若函数 y=(m−1)x|m|+3 是一次函数，则m= ， 且 随 的增大而

    查看试题解析

  • 15. 某班带队到展览馆参观，并要求作好记录，小亮随队伍步行一段时间后，发现未带笔记本，随即跑步返回拿到笔记本后又以相同的速度追赶队伍，恰好与队伍在同一时间到达展览馆．行程与时间的关系如图所示，其中实线表示队伍的图象，虚线表示小亮的图象，则小亮跑步的速度为米/分钟．


    查看试题解析

三、解答题

  • 16. 某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如下表：

    若日销售量y是销售价x的一次函数．

    x （元）

    15

    20

    25

    …

    y （件）

    25

    20

    15

    …

    (1)、求出日销售量y（件）与销售价x（元）的函数关系式；
    (2)、求销售价定为30元时，每日的销售利润．

    查看试题解析

  • 17. 已知一次函数 y=(4+2m)x+m−4 ，求：
    (1)、m为何值时，y随 x 的增大而减少？ 
    (2)、m为何值时，函数图象与y轴的交点在 x 轴下方？
    (3)、m为何值时，图象经过第一、三、四象限？ 
    (4)、图象能否过第一、二、三象限？

    查看试题解析

四、综合题

  • 18. 某通讯公司推出①、②两种收费方式供用户选择，其中一种有月租费，另一种无月租费，且两种收费方式的通讯时间x（分钟）与收费y（元）之间的函数关系如图所示．

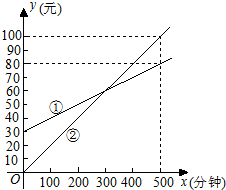    (1)、分别求出①、②两种收费方式中y与自变量x之间的函数关系式；
    (2)、何时两种收费方式费用相等？

    查看试题解析

  • 19.

    小明从家骑自行车出发，沿一条直路到相距2400m的邮局办事，小明出发的同时，他的爸爸以96m/min的速度从邮局沿同一条道路步行回家，小明在邮局停留2min后沿原路以原速返回，设他们出发后经过t min时，小明与家之间的距离为 S1 m，小明爸爸与家之间的距离为S2 m，图中折线OABD，线段EF分别是表示S1、S2与t之间函数关系的图像．

    （1）求S2与t之间的函数关系式：
    （2）小明从家出发，经过多长时间在返回途中追上爸爸？这时他们距离家还有多远？

    查看试题解析

  • 20. 如图，在平面直角坐标系xOy中，一次函数y＝k1x＋b的图象与x轴交于点A（－3，0），与y轴交于点B，且与正比例函数y＝kx的图象交点为C（3，4）．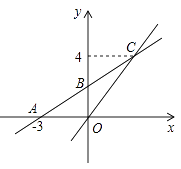


    (1)、求正比例函数与一次函数的关系式；
    (2)、若点D在第二象限，△DAB是以AB为直角边的等腰直角三角形，请求出点D的坐标；
    (3)、在x轴上是否存在一点E使△BCE周长最小，若存在，求出点E的坐标
    (4)、在x轴上求一点P使△POC为等腰三角形，请直接写出所有符合条件的点P的坐标．

    查看试题解析