江苏省镇江市丹阳市2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-04-19 类型:期末考试
一、填空题
-
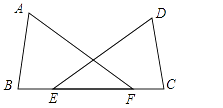
1. 比较大小: (填“ ”、“ ”、“ ”).2. 平面直角坐标系中,点 关于 轴的对称点的坐标是.3. 若一个等腰三角形的顶角等于 ,则它底角等于 .4. 如图,已知B、E、F、C在同一直线上,BE=CF,AF=DE,则添加条件 , 可以判断△ABF≌△DCE.
 5. 一个等腰三角形的两边长分别为 和 ,则它的周长为 .6. 已知点P(a,b)在一次函数y=2x﹣1的图象上,则4a﹣2b+1=.7. 如图,在 中, 和 的平分线相交于点 ,过 作 ,交 于点 ,交 于点 .若 ,则线段 的长为.
5. 一个等腰三角形的两边长分别为 和 ,则它的周长为 .6. 已知点P(a,b)在一次函数y=2x﹣1的图象上,则4a﹣2b+1=.7. 如图,在 中, 和 的平分线相交于点 ,过 作 ,交 于点 ,交 于点 .若 ,则线段 的长为.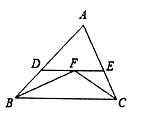 8. 如图,在Rt△ABC中,∠BAC=90°,AC的垂直平分线分别交BC、AC于点D,E,若AB=5cm,AC=12cm,则△ABD的周长为cm.
8. 如图,在Rt△ABC中,∠BAC=90°,AC的垂直平分线分别交BC、AC于点D,E,若AB=5cm,AC=12cm,则△ABD的周长为cm. 9. 如图,两条直线 和 的关系式分别为 ,两直线的交点坐标为 ,当 时, 的取值范围为.
9. 如图,两条直线 和 的关系式分别为 ,两直线的交点坐标为 ,当 时, 的取值范围为. 10. 若直角三角形斜边上的高和中线长分别是4cm,5cm,则它的面积是cm2.11. 如图,在 中, ,点 在射线 上,且 ,则 .
10. 若直角三角形斜边上的高和中线长分别是4cm,5cm,则它的面积是cm2.11. 如图,在 中, ,点 在射线 上,且 ,则 .
二、单选题
-
12. 在下列各数中,无理数是( )A、 B、 C、 D、13. 下列四组数,可作为直角三角形三边长的是( )A、 、 、 B、 、 、 C、 、 、 D、 、 、14. 如果点P(m,1﹣2m)在第一象限,那么m的取值范围是( )A、 B、 C、 D、15. 如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为用A、B.下列结论中不一定成立的是( )
 A、PA=PB B、PO平分∠APB C、AB垂直平分OP D、OA=OB16. 如图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=34°,那么∠BED=( )
A、PA=PB B、PO平分∠APB C、AB垂直平分OP D、OA=OB16. 如图,已知AE平分∠BAC,BE⊥AE于E,ED∥AC,∠BAE=34°,那么∠BED=( )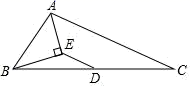 A、134° B、124° C、114° D、104°17. 一次函数 的图象与 轴、 轴交于 两点,点 是坐标平面内直线 外一点,过点 作 轴的平行线交直线 于点 ,过点 作 轴的平行线交直线 于点 ,则 ( )A、 B、 C、 D、
A、134° B、124° C、114° D、104°17. 一次函数 的图象与 轴、 轴交于 两点,点 是坐标平面内直线 外一点,过点 作 轴的平行线交直线 于点 ,过点 作 轴的平行线交直线 于点 ,则 ( )A、 B、 C、 D、三、解答题
-
18. 计算:(1)、(2)、19. 求下列各式中的 的值:(1)、(2)、20. 如图, ,

求证:
(1)、 ;(2)、 .21. 如图,在△ABC中,AD⊥BC,AD=12,BD=16,CD=5.求△ABC的周长: 22. 已知一次函数y=kx+b的图象过(1,1)和(2,−1).(1)、求一次函数y=kx+b的解析式;(2)、求直线y=kx+b与坐标轴围成的三角形的面积。23. 如图,在 中,边 的垂直平分线 与边 的垂直平分线 交于点 这两条垂直平分线分别交 于点 .
22. 已知一次函数y=kx+b的图象过(1,1)和(2,−1).(1)、求一次函数y=kx+b的解析式;(2)、求直线y=kx+b与坐标轴围成的三角形的面积。23. 如图,在 中,边 的垂直平分线 与边 的垂直平分线 交于点 这两条垂直平分线分别交 于点 . (1)、若 ,求 的度数;(2)、已知 的周长 ,分别连接 ,若 的周长为 ,求 的长.24. 某地区的电力资源缺乏,未能得到较好的开发.该地区一家供电公司为了居民能节约用电,采用分段计费的方法来计算电费.月用电量 (度)与相应电费 (元)之间的函数图象如图所示.
(1)、若 ,求 的度数;(2)、已知 的周长 ,分别连接 ,若 的周长为 ,求 的长.24. 某地区的电力资源缺乏,未能得到较好的开发.该地区一家供电公司为了居民能节约用电,采用分段计费的方法来计算电费.月用电量 (度)与相应电费 (元)之间的函数图象如图所示. (1)、月用电量为 度时,应交电费多少元?(2)、当 时,求 与 之间的函数关系式;(3)、月用电量为 度时,应交电费多少元?25. 某校机器人兴趣小组在如图所示的三角形场地上开展训练.已知: 中, ;机器人从点 出发,沿着 边按 的方向匀速移动到点 停止;机器人移动速度为每秒 个单位,移动至拐角处调整方向需要 秒(即在 处拐弯时分别用时 秒).设机器人所用时间为 秒时,其所在位置用点 表示(机器人大小不计).
(1)、月用电量为 度时,应交电费多少元?(2)、当 时,求 与 之间的函数关系式;(3)、月用电量为 度时,应交电费多少元?25. 某校机器人兴趣小组在如图所示的三角形场地上开展训练.已知: 中, ;机器人从点 出发,沿着 边按 的方向匀速移动到点 停止;机器人移动速度为每秒 个单位,移动至拐角处调整方向需要 秒(即在 处拐弯时分别用时 秒).设机器人所用时间为 秒时,其所在位置用点 表示(机器人大小不计). (1)、点 到边 的距离是;(2)、是否存在这样的时刻,使 为等腰三角形?若存在,求出 的值;若不存在,请说明理由.26. (问题背景)
(1)、点 到边 的距离是;(2)、是否存在这样的时刻,使 为等腰三角形?若存在,求出 的值;若不存在,请说明理由.26. (问题背景)平移、旋转和翻折是初中阶段三大基本几何变换.平移、旋转或翻折后的图形与原图形全等,所以我们又把这些几何变换称之保形变换.我市某校数学思维社团成员在学习了平面直角坐标系及一次函数以后,尝试在平面直角坐标系中研究几何变换.
(1)、(初步研究)本着简单到复杂的原则,他们先研究了点的变换:已知平面内一点 .
①将点 向左平移 个单位,平移后点 的坐标为 ;
②点 关于直线 的对称点的坐标为;
③将点 绕点 旋转 ,旋转后点 的坐标为;
(2)、(初步研究)数学思维社团成员认为线的变换只要抓住一些关键点的变换就可以了.已知如图,直线 分别与 轴、 轴交于点 两点,直线 交直线 于点 .

①直线 向右平移 个单位,平移后的直线表达式为;
②将直线 沿直线 翻折,翻折后的直线表达式为;
③将直线 绕点 旋转 ,旋转后的直线表达式为 ;
④将直线 绕点 逆时针旋转 ,添加一个你认为合适的角度 ;并直接写出旋转后的直线表达式 .
27. (定义)如果 条线段将一个三角形分成 个等腰三角形,那么这 条线段就称为这个三角形的“二分等腰线”,如果 条线段将一个三角形分成 个等腰三角形,那么这 条线段就称为这个三角形的“三分等腰线”.
(1)、(理解)如图(1),在 中, ,请你在这个三角形中画出它的“二分等腰线”,不限作法,请在图中标出等腰三角形顶角的度数.
 (2)、如图(2),已知 是一个顶角为 的等腰三角形,请你在这个三角形中画出它的“三分等腰线”,不限作法,请在图中标出所分得的等腰三角形底角的度数.
(2)、如图(2),已知 是一个顶角为 的等腰三角形,请你在这个三角形中画出它的“三分等腰线”,不限作法,请在图中标出所分得的等腰三角形底角的度数. (3)、(应用)
(3)、(应用)小明在学习了上面的材料后得到一个结论:直角三角形一定存在“二分等腰线”;而小丽则认为直角三角形也一定存在“三分等腰线”.
①你认为直角三角形的 就是它的“二分等腰线”;
②如图(3),在 中, ,请你在图(3)中帮助小丽画出 的“三分等腰线”(要求:尺规作图,不写作法,保留作图痕迹).

(4)、在 中, 和 分别是 的“三分等腰线”,点 在边 上,点 在 边上,且 ,请根据题意写出 度数的所有可能的值.