江苏省盐城市滨海县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 有 两根木条,现想找一根木条组成直角三角形,则下列木条长度适合的是( )A、8cm B、12cm C、18cm D、20cm3. 下列实数是无理数的是( )A、0.5 B、 C、1 D、4. 下列数据不能确定物体位置的是( )A、电影票5排8号 B、东经 北纬 C、希望路25号 D、北偏东5. 下列条件中能作出唯一三角形的是( )A、AB=4cm,BC=3cm,AC=5cm B、AB=2cm,BC=6cm,AC=4cm C、∠A=∠B=∠C=60° D、∠A=30°,∠B=60°,∠C=90°6. 如图,在△ABC中,AB=AC,∠A=42°,DE垂直平分AC,则∠BCD的度数为( )
2. 有 两根木条,现想找一根木条组成直角三角形,则下列木条长度适合的是( )A、8cm B、12cm C、18cm D、20cm3. 下列实数是无理数的是( )A、0.5 B、 C、1 D、4. 下列数据不能确定物体位置的是( )A、电影票5排8号 B、东经 北纬 C、希望路25号 D、北偏东5. 下列条件中能作出唯一三角形的是( )A、AB=4cm,BC=3cm,AC=5cm B、AB=2cm,BC=6cm,AC=4cm C、∠A=∠B=∠C=60° D、∠A=30°,∠B=60°,∠C=90°6. 如图,在△ABC中,AB=AC,∠A=42°,DE垂直平分AC,则∠BCD的度数为( ) A、23° B、25° C、27° D、29°7. 如图, 平分 , 于点 ,点 是射线 上的一个动点,若 ,则PE的最小值( )
A、23° B、25° C、27° D、29°7. 如图, 平分 , 于点 ,点 是射线 上的一个动点,若 ,则PE的最小值( ) A、等于 B、大于 C、小于 D、无法确定8. 2020年10月1日,小明乘大客车到大丰“荷兰花海”看郁金香花海,早上,大客车从滨海出发到大丰,匀速行驶一段时间后,途中遇到堵车原地等待一会儿,然后大客车加快速度行驶,按时到达“荷兰花海”.参观结束后,大客车匀速返回.其中x表示小明所乘客车从滨海出发后至回到滨海所用的时间,y表示客车离滨海的距离,下面能反映y与x的函数关系的大致图象是( )A、
A、等于 B、大于 C、小于 D、无法确定8. 2020年10月1日,小明乘大客车到大丰“荷兰花海”看郁金香花海,早上,大客车从滨海出发到大丰,匀速行驶一段时间后,途中遇到堵车原地等待一会儿,然后大客车加快速度行驶,按时到达“荷兰花海”.参观结束后,大客车匀速返回.其中x表示小明所乘客车从滨海出发后至回到滨海所用的时间,y表示客车离滨海的距离,下面能反映y与x的函数关系的大致图象是( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
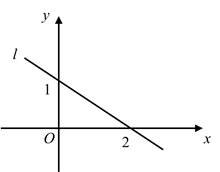
9. 化简: = .10. 一个三角形的三边为6、10、x,另一个三角形的三边为 、6、12,如果这两个三角形全等,则 =.11. 已知等腰三角形的两边长分别为4和8,则它的周长是 .12. 在直角三角形ABC中,斜边AB=2,则AB2+AC2+BC2= .13. 已知点 ,点 关于y轴对称,则 .14. 如图,直线 是一次函数 ( )的图象,则 .
 15. 如图,AD是等边 ABC的中线,E是AC上一点,且AD=AE,则∠EDC=°
15. 如图,AD是等边 ABC的中线,E是AC上一点,且AD=AE,则∠EDC=° 16. 如图,已知方格纸中是4个相同的小正方形,则 的度数为.
16. 如图,已知方格纸中是4个相同的小正方形,则 的度数为.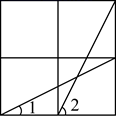 17. 小明从家跑步到学校,接着立即原路步行回家.如图是小明离家的路程y(米)与时间x(分)之间的函数关系的图象,则小明步行回家的平均速度是米/分.
17. 小明从家跑步到学校,接着立即原路步行回家.如图是小明离家的路程y(米)与时间x(分)之间的函数关系的图象,则小明步行回家的平均速度是米/分. 18. 某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如表:
18. 某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如表:t(小时)
0
1
2
3
y(升)
120
112
104
96
由表格中y与t的关系可知,当汽车行驶小时,油箱的余油量为0.
三、解答题
-
19. 计算:(1)、(2)、20. 若 是9的算术平方根, 的立方根是 ,求 的值.21. 如图, , , .求证: .
 22. 已知一次函数 的图象经过点(4,0).
22. 已知一次函数 的图象经过点(4,0).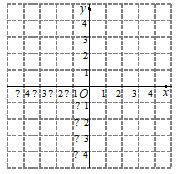 (1)、求k的值;(2)、画出该函数的图象;(3)、点P是该函数图象上一个动点,连接OP,则OP的最小值是.23. 如图,在平面直角坐标系中,已知A(10,0),B(10,6),BC⊥y轴,垂足为C,点D在线段BC上,且AD=AO.
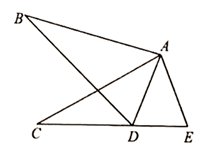
(1)、求k的值;(2)、画出该函数的图象;(3)、点P是该函数图象上一个动点,连接OP,则OP的最小值是.23. 如图,在平面直角坐标系中,已知A(10,0),B(10,6),BC⊥y轴,垂足为C,点D在线段BC上,且AD=AO.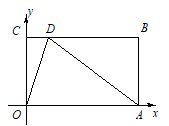 (1)、试说明:DO平分∠CDA;(2)、求点D的坐标.24. 定义:如图,点M、N把线段 分割成 、 和 ,若以 、 、 为边的三角形是一个直角三角形,则称点M、N是线段 的勾股分割点.已知点M、N是线段 的勾股分割点,若 , ,求 的长.
(1)、试说明:DO平分∠CDA;(2)、求点D的坐标.24. 定义:如图,点M、N把线段 分割成 、 和 ,若以 、 、 为边的三角形是一个直角三角形,则称点M、N是线段 的勾股分割点.已知点M、N是线段 的勾股分割点,若 , ,求 的长. 25. 某县在创建省文明卫生城市中,绿化档次不断提升.某校计划购进A、B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元(1)、求A种、B种树木每棵各多少元?(2)、因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价八折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.26. 设一次函数 ( )的图象为直线 ,一次函数 ( )的图象为直线 ,若 ,且 ,我们就称直线 与直线 互相平行.解答下面的问题:
25. 某县在创建省文明卫生城市中,绿化档次不断提升.某校计划购进A、B两种树木共100棵进行校园绿化升级,经市场调查:购买A种树木2棵,B种树木5棵,共需600元;购买A种树木3棵,B种树木1棵,共需380元(1)、求A种、B种树木每棵各多少元?(2)、因布局需要,购买A种树木的数量不少于B种树木数量的3倍.学校与中标公司签订的合同中规定:在市场价格不变的情况下(不考虑其他因素),实际付款总金额按市场价八折优惠,请设计一种购买树木的方案,使实际所花费用最省,并求出最省的费用.26. 设一次函数 ( )的图象为直线 ,一次函数 ( )的图象为直线 ,若 ,且 ,我们就称直线 与直线 互相平行.解答下面的问题: (1)、求过点 且与已知直线 平行的直线l的函数表达式;(2)、设(1)中的直线l分别与x轴、y轴交于A、B两点,直线 分别与x轴、y轴交于C、D两点,求四边形 的面积.27. 如图,直线 与坐标轴分别交于A、B两点,OA=8,OB=6.动点P从O点出发,沿路线O→A→B以每秒2个单位长度的速度运动,到达B点时运动停止.
(1)、求过点 且与已知直线 平行的直线l的函数表达式;(2)、设(1)中的直线l分别与x轴、y轴交于A、B两点,直线 分别与x轴、y轴交于C、D两点,求四边形 的面积.27. 如图,直线 与坐标轴分别交于A、B两点,OA=8,OB=6.动点P从O点出发,沿路线O→A→B以每秒2个单位长度的速度运动,到达B点时运动停止.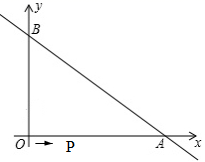 (1)、则A点的坐标为 , B两点的坐标为;(2)、当点P在OA上,且BP平分∠OBA时,则此时点P的坐标为;(3)、设点P的运动时间为t秒(0≤t≤4),△BPA的面积为S,求S与t之间的函数关系式:并直接写出当S=8时点P的坐标.
(1)、则A点的坐标为 , B两点的坐标为;(2)、当点P在OA上,且BP平分∠OBA时,则此时点P的坐标为;(3)、设点P的运动时间为t秒(0≤t≤4),△BPA的面积为S,求S与t之间的函数关系式:并直接写出当S=8时点P的坐标.