江苏省南通市海安市2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 下列式子是最简二次根式的是( )A、 B、 C、 D、2. 如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快就画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )
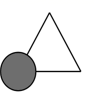 A、AAS B、ASA C、SAS D、SSS3. 下列代数式变形正确的是( )A、 B、 C、 D、4. 对于① ,② ,从左到右的变形,表述正确的是( )A、都是因式分解 B、①是因式分解,②是乘法运算 C、都是乘法运算 D、①是乘法运算,②是因式分解5. 在平面直角坐标系中,点A的坐标是(– 1,2),作点A关于y轴的对称点,得到点A',再将点A'向下平移4个单位,得到点A″,则点A″的坐标是()A、(– 1,– 2) B、(1,2) C、(1,– 2) D、(–2,1)6. 如图, 中, ,点 在边 上(不与顶点 重合),则 的度数可能是( )
A、AAS B、ASA C、SAS D、SSS3. 下列代数式变形正确的是( )A、 B、 C、 D、4. 对于① ,② ,从左到右的变形,表述正确的是( )A、都是因式分解 B、①是因式分解,②是乘法运算 C、都是乘法运算 D、①是乘法运算,②是因式分解5. 在平面直角坐标系中,点A的坐标是(– 1,2),作点A关于y轴的对称点,得到点A',再将点A'向下平移4个单位,得到点A″,则点A″的坐标是()A、(– 1,– 2) B、(1,2) C、(1,– 2) D、(–2,1)6. 如图, 中, ,点 在边 上(不与顶点 重合),则 的度数可能是( ) A、 B、 C、 D、7. 化简 的结果是( )A、 B、 C、 D、18. 如图①,已知 ,用尺规作它的角平分线(如图②).
A、 B、 C、 D、7. 化简 的结果是( )A、 B、 C、 D、18. 如图①,已知 ,用尺规作它的角平分线(如图②).
尺规作图具体步骤如下,
第1步:以 为圆心,以 为半径画弧,分别交射线 于点 ;
第2步:分别以 为圆心,以 为半径画弧,两弧在 内部交于点 ;
第3步:画射线 .射线 即为所求.
下列说法正确的是( )
A、 有最小限制, 无限制 B、 的长 C、 的长 D、连接 ,则 垂直平分9. 已知: 是整数, .设 .则符合要求的 的正整数值共有( )A、1个 B、2个 C、3个 D、4个10. 如图,在 中, 平分 .边 的垂直平分线 分别交 于点 .以下说法错误的是( )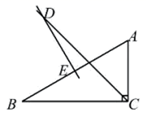 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若根式 在实数范围内有意义,则 的取值范围是.12. 若分式 的值为0,则x= .13. 化简 的结果为.14. 如果点 与点 关于 轴对称,则 的值为.15. 如图, 是 的角平分线, ,则点 到 的距离为.
 16. 如图, 中, ,若 是 的中点, ,垂足是 ,则 的值等于.
16. 如图, 中, ,若 是 的中点, ,垂足是 ,则 的值等于. 17. 一辆汽车以 的速度由甲市驶往乙市,然后以 的速度返回,那么汽车往返两市的平均速度是(用含 的式子表示).18. 旧知回顾:在七年级学习“平方根”时,我们会直接开方解形如 的方程(解为 ).解题运用:方程 解为.
17. 一辆汽车以 的速度由甲市驶往乙市,然后以 的速度返回,那么汽车往返两市的平均速度是(用含 的式子表示).18. 旧知回顾:在七年级学习“平方根”时,我们会直接开方解形如 的方程(解为 ).解题运用:方程 解为.三、解答题
-
19. 计算:(1)、 ;(2)、 ;(3)、 ;(4)、 .20. 先化简,再求值: ,其中 .21. 如图,平面直角坐标系 中,有五个点 .
 (1)、哪两个点关于 轴对称?(直接填写答案);(2)、在 轴上找一个点 ,使点 到点 的距离之和最短(画出示意图即可,不需要说明理由).22.(1)、判断下列各式是否成立?并选择其中一个说明理由;
(1)、哪两个点关于 轴对称?(直接填写答案);(2)、在 轴上找一个点 ,使点 到点 的距离之和最短(画出示意图即可,不需要说明理由).22.(1)、判断下列各式是否成立?并选择其中一个说明理由;; ; .
(2)、用字母表示(1)中式子的规律,并给出证明.23. 如图,在 中, 是它的角平分线. (1)、求证: ;(2)、若 ,求 的长.24. 列方程解应用问题:甲、乙两个小组同时开始登山.(1)、若山高 ,甲组的攀登速度(单位: )是乙组的1.2倍,甲组比乙组早 到达山顶.求甲组的攀登速度;(2)、如果山高为 ,甲组的攀登速度(单位: )是乙组的 倍,甲组比乙组早 到达山顶.求乙组的攀登速度.25. 如图,在 中, ,点 是边 上的动点,连接 ,点 关于直线 的对称点为点 ,射线 与直线 交于点 .
(1)、求证: ;(2)、若 ,求 的长.24. 列方程解应用问题:甲、乙两个小组同时开始登山.(1)、若山高 ,甲组的攀登速度(单位: )是乙组的1.2倍,甲组比乙组早 到达山顶.求甲组的攀登速度;(2)、如果山高为 ,甲组的攀登速度(单位: )是乙组的 倍,甲组比乙组早 到达山顶.求乙组的攀登速度.25. 如图,在 中, ,点 是边 上的动点,连接 ,点 关于直线 的对称点为点 ,射线 与直线 交于点 .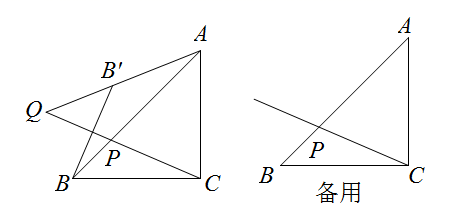 (1)、当 时,求 的度数;(2)、当 时,连接 ,求证: ;(3)、当 时,猜想 和 的数量关系,并证明.26. (阅读材料)
(1)、当 时,求 的度数;(2)、当 时,连接 ,求证: ;(3)、当 时,猜想 和 的数量关系,并证明.26. (阅读材料)小慧同学数学写作片段
乘法公式“大家族”
学习《整式的乘法及因式分解》之后,我发现乘法公式不只是教材上“黑体字”明确的“平方差公式 ”“完全平方公式 和 ”,其实在教材或平时的练习中还“隐含”一些“乘法公式”值得积累,比如,
;
;
;
.
……
(解题运用)
(1)、在实数范围内因式分解: ;(2)、设 满足等式 ,求 的值;(3)、若正数 满足等式 ,求代数式 的值.