江苏省南京市溧水区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 4的平方根是（）

A、 2 B、 $- 2$ C、 $\pm 2$ D、4

查看试题解析
2. 在平面直角坐标系中，下列位于第二象限的点是（）

A、（1 ，2） B、（－2 ，3） C、（0 ，0） D、（2 ，－3）

查看试题解析
3. 要调查溧水区中学生了解禁毒知识的情况，下列抽样调查最适合的是（）

A、在溧水区某中学随机抽取200名女生 B、在溧水区中学生中随机抽取200名男生 C、在溧水区中学生中随机抽取200名学生 D、在溧水区某中学随机抽取200名学生

查看试题解析
4. 小华在镜中看到身后墙上的钟，你认为实际时间最接近8点的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，点B、C、E在同一条直线上，∠B＝∠E＝∠ACF＝60°，AB＝CE，则下列与BC相等的线段是（）

A、AC B、AF C、CF D、EF

查看试题解析
6. 已知方程 $k x + b = 0$ 的解是 $x = 3$ ，则一次函数的图象可能是（）

A、 B、 C、 D、

查看试题解析
7. 如图，在△ABC中，AB=8，AC=6，BC边的垂直平分线交AB于E，交BC于点D，若CD=5，则AE的长为（）

A、 $\frac{7}{4}$ B、2 C、 $\frac{21}{4}$ D、4

查看试题解析
8. 如图①，在Rt△ABC中，∠ACB＝90°，D是斜边AB的中点，动点P从B点出发，沿B→C→A运动，设S_△PDB＝y，点P运动的路程为x，若y与x之间的函数图象如图②所示，则AC的长为（）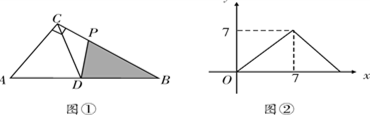

A、14 B、7 C、4 D、2

查看试题解析

二、填空题

9. $| - \sqrt{7} |$ ＝.

查看试题解析
10. 比较大小： $\sqrt{17} - 1$ 3.（填“ $>$ ”“ $<$ ”或“＝”号）

查看试题解析
11. 某校在七年级入学时抽取了部分男生测量身高，结果统计身高（单位：m ）在1.35~1.42这一小组的频数为40人，频率为0.2，则抽取的男生共有人.

查看试题解析
12. 在平面直角坐标系中，将点M（3，-1）沿x轴向左平移2个单位，再沿y轴向下平移3个单位后得到点N，则点N的坐标为.

查看试题解析
13. 函数y＝kx－4的值y随x的增大而减小，写出一个符合上述条件的k的值：.

查看试题解析
14. 在 $R t △ A B C$ 中， $∠ C ＝ 90 ° ， A B ＝ 25 ， A C ＝ 7$ ，则△ABC的面积为.

查看试题解析
15. 如图，已知一次函数 $y_{1} = x + b$ 与一次函数 $y_{2} = mx - n$ 的图象相交于点P（-2，1），则关于x的不等式x+b≥mx-n的解集为.

查看试题解析
16. 如图，在平面直角坐标系中，以A（2，0），B（0，1）为顶点作等腰直角三角形ABC（其中∠ABC＝90°，且点C落在第一象限），则点C关于y轴的对称点C'的坐标为.

查看试题解析
17. 已知：如图△ABC中，∠B＝50°，∠C＝90°，在射线BA上找一点D，使△ACD为等腰三角形，则∠ACD的度数为.

查看试题解析
18. 如图，点A、B、C在一次函数y＝﹣2x+m的图象上，它们的横坐标依次为﹣1、1、2，分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积的和是.

查看试题解析

三、解答题

19.

(1)、计算（－1）²⁰²⁰ $- \sqrt{9}$ $+ \sqrt[3]{- 8}$ .

(2)、求（x＋1）²－49＝0中x的值.

查看试题解析
20. 如图，∠ADB＝∠ADC，∠B＝∠C.

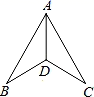(1)、求证：AB＝AC；

(2)、连接BC，求证：AD⊥BC.

查看试题解析
21. 为响应党的“文化自信”号召，我区某校开展了古诗词诵读大赛活动.现随机抽取部分同学的成绩进行统计，并绘制成如下的两个不完整的统计图.请结合图中提供的信息，解答下列各题：

(1)、本次抽取的学生共人；

(2)、直接写出a的值：，并把频数分布直方图补充完整.

(3)、如果全校有2000名学生参加这次活动，80分以上（含80分）为良好，那么估计全校获得良好奖的学生有多少人?

查看试题解析
22. 已知一次函数y＝kx＋b.当x＝－3时，y＝－8；当x＝0时，y＝－4.

(1)、求该一次函数的表达式；

(2)、求该函数的图象与坐标轴围成的图形的面积.

查看试题解析
23. 如图，学校有一块三角形空地ABC，计划将这块三角形空地分割成四边形ABDE和△EDC，分别摆放“秋海棠”和“天竺葵”两种不同的花卉.经测量，∠EDC＝90°，DC＝6m，CE＝10 m，BD＝14 m，AB＝16m，AE＝2m.

(1)、求DE的长；

(2)、求四边形ABDE的面积.

查看试题解析
24. 问题：如图①，要在一条笔直的路边l上建一个燃气站，向l同侧的A、B两个城镇分别铺设管道输送燃气.试确定燃气站的位置，使铺设管道的路线最短.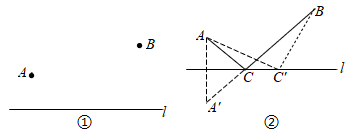

(1)、如图②，作出点A关于l的对称点A'，线段A'B与直线l的交点C的位置即为所求，即在点C处建燃气站，所得路线ACB是最短的.
为了证明点C的位置即为所求，不妨在直线l上另外任取一点C'，连接AC'、BC'，证明AC＋CB＜AC'＋C'B.请完成这个证明.

(2)、如图③，点P为∠MON内的一个定点，在OM上有一点A，ON上有一点B.请你作出点A和点B的位置，使得△PAB的周长最小.（保留作图痕迹，不写作法）在上述条件下，若∠MON＝40°，则∠APB＝°.

查看试题解析
25. A，B两地相距100千米，甲，乙两人骑车分别从A，B两地相向而行，图中 $l_{1}$ 和 $1_{2}$ 分别表示他们各自到A地的距离 $y ($ 千米 $)$ 与时间 $x ($ 小时 $)$ 的关系，根据图中提供的信息，解答下列问题：

(1)、图中哪条线表示甲到A地的距离与时间的关系？

(2)、甲，乙两人的速度分别是多少？

(3)、求P点的坐标，并解释P点的实际意义.

(4)、甲出发多长时间后，两人相距30千米？

查看试题解析
26.

(1)、（探索研究）
老师在课堂上给出了这样一道题目：如图，在△ABC中，AB＝AC，∠BAC＝90°，CD平分∠ACB，BE⊥CD，垂足E在CD的延长线上.试探究线段BE和CD的数量关系.小明同学经过认真思考后认为：先延长CA、BE相交于点为F，再证明△ACD≌△ABF即可，请根据小明同学的思路补全图形并直接写出线段BE和CD的数量关系.

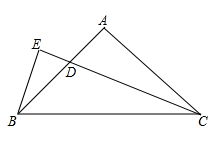(2)、（类比探究）
老师引导同学们继续研究：

如图，在△ABC中，AB＝AC，∠BAC＝90°，点D在线段BC上，∠EDB＝ $\frac{1}{2}$ ∠C，BE⊥DE，垂足为E，DE与AB相交于点F，试探究线段BE与FD的数量关系，并证明你的结论.

查看试题解析