湖南省岳阳市华容县2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列代数式中，是分式的为（）

A、 $\frac{x}{3}$ B、 $\frac{y}{π}$ C、 $\frac{x}{3} - \frac{y}{2}$ D、 $\frac{2}{x - y}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{16} = \pm 4$ B、 $a^{8} \div a^{2} = a^{4}$ C、 ${(a^{- 3})}^{- 2} = a^{- 5}$ D、 ${(\frac{x}{y^{3}})}^{3} = \frac{x^{3}}{y^{9}}$

查看试题解析
3. 已知不等式组 ${\begin{matrix} x - 2 < 0 \\ x + 1 \geq 0 \end{matrix}$ ，其解集在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
4. 计算 $\sqrt{8} + \sqrt{18}$ 的结果是（）

A、 $\sqrt{26}$ B、 $2 \sqrt{5}$ C、 $5 \sqrt{2}$ D、 $7 \sqrt{2}$

查看试题解析
5. 等腰三角形的两边长分别为 $4 cm$ ， $8 cm$ ，则该三角形的周长为（）

A、 $16 cm$ B、 $20 cm$ C、 $16 cm$ 或 $20 cm$ D、以上都不对

查看试题解析
6. 如图，点P是AB上任意一点，∠ABC=∠ABD，还应补充一个条件，才能推出△APC≌△APD．从下列条件中补充一个条件，不一定能推出△APC≌△APD的是（）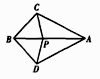

A、BC=BD； B、AC=AD； C、∠ACB=∠ADB； D、∠CAB=∠DAB

查看试题解析
7. 下列命题是假命题的是（）

A、线段垂直平分线上的点到线段两端的距离相等 B、三角形的一个外角等于与它不相邻的两个内角的和 C、有一个外角是120°的等腰三角形是等边三角形 D、有两边和一角对应相等的两个三角形全等

查看试题解析
8. 若关于x的一元一次不等式 ${\begin{array}{l} \frac{3 x - 1}{2} \leq x + 3 \\ x \leq a \end{array}$ 的解集为 $x \leq a$ ；且关于 $y$ 的分式方程 $\frac{y - a}{y - 2} + \frac{3 y - 4}{y - 2} = 1$ 有正整数解，则所有满足条件的整数a的值之积是（）

A、7 B、－14 C、28 D、－56

查看试题解析

二、填空题

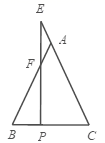
9. 当x时，分式 $\frac{1}{x + 3}$ 有意义.

查看试题解析
10. 根据资料显示，新冠病毒的直径最小大约为 $0.00000008$ 米，这个数用科学记数法表示为.

查看试题解析
11. 在3.14，0， $- \frac{π}{5}$ ， $\sqrt{2}$ ， $- \frac{22}{7}$ ，2.010010001…（每两个1之间的0依次增加1个）中，无理数有个.

查看试题解析
12. 若｜a-2|+ $\sqrt{b + 3}$ +(c-4)²=0，则a-b+c=.

查看试题解析
13. 如图，在 $△ A B C$ 中， $A B = A C$ ，点 $E$ 在 $C A$ 延长线上， $E P ⊥ B C$ 于点 $P$ ，交 $A B$ 于点 $F$ ，若 $C E = 10$ ， $A F = 3$ ，则 $B F$ 的长度为.

查看试题解析
14. 已知实数 $a = \sqrt{3} - 1$ ，则a的倒数为.

查看试题解析
15. 已知关于 $x$ 的方程 $\frac{x - 4}{x - 3} - k - 4 = \frac{k}{3 - x}$ 无解，则k的值为.

查看试题解析
16. 如图， $A D$ 是 $Δ A B C$ 的中线， $E$ 、 $F$ 分别是 $A D$ 和 $A D$ 延长线上的点，且 $D E = D F$ ，连接 $B F$ 、 $C E$ ，下列说法：① $Δ A B D$ 和 $Δ A C D$ 的面积相等，② $∠ B A D = ∠ C A D$ ，③ $Δ B D F ≅ Δ C D E$ ，④ $B F / / C E$ ，⑤ $C E = B F$ ，其中一定正确的答案有．（只填写正确的序号）

查看试题解析

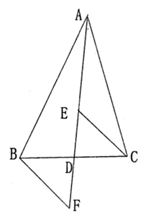
三、解答题

17. 计算： ${(π - \sqrt{2})}^{0} - {(\frac{1}{2})}^{- 2} + \sqrt[3]{- 8} - | 1 - \sqrt{2} |$ .

查看试题解析
18. 解方程： $\frac{3}{x + 1} = \frac{x}{2 x + 2}$ +1．

查看试题解析
19. 已知 $A = \frac{x^{2} + 2 x + 1}{x^{2} - 1} - \frac{x}{x - 1}$ .

(1)、化简A；

(2)、当 $x$ 满足不等式组 ${\begin{array}{l} x - 1 \geq 0 \\ x - 3 < 0 \end{array}$ ，且 $x$ 为整数时，求A的值.

查看试题解析
20. 如图，在△ABC中，AB=AC，CD⊥AB于点D，BE⊥AC于点E．求证：BE=CD．

查看试题解析
21. 第5代移动通信技术简称5G，某地已开通5G业务，经测试5G下载速度是4G下载速度的15倍，明明和芳芳分别用5G与4G下载一部600兆的公益片，明明比芳芳所用的时间快 $\frac{7}{3}$ 分钟，求该地4G与5G下载速度分别是每秒多少兆？

查看试题解析
22. 如图，在△ABC中，AB=AC， $A B$ 的垂直平分线交 $A C$ 于点 $E$ .

(1)、已知 $∠ A = 40 °$ ，求 $∠ C B E$ 的度数；

(2)、已知 $△ B C E$ 的周长为 $8 cm$ ， $A C - B C = 2$ ，求 $A B$ 与 $B C$ 的长.

查看试题解析
23. 阅读材料：一些含根号的式子可以写成另一个含根号的式子的平方，如 $3 + 2 \sqrt{2} = {(1 + \sqrt{2})}^{2}$ 其思考过程如下：
设 $a + \sqrt{2} b = {(m + \sqrt{2} n)}^{2}$ （其中 $a ， b ， m ， n$ 均为正整数）则有 $a + \sqrt{2} b = m^{2} + 2 \sqrt{2} m n + 2 n^{2}$ ，∴ $a = m^{2} + 2 n^{2}$ ， $b = 2 m n .$

请你解决问题：

(1)、当 $a ， b ， m ， n$ 均为正整数时，若 $a + \sqrt{3} b = {(m + \sqrt{3} n)}^{2}$ ，用含 $m ， n$ 的式子分别表示 $a$ ， $b$ 得： $a$ = ， $b$ =.

(2)、利用所探索的结论，找一组正整 $a ， b ， m ， n$ 填空：
+ $\sqrt{3}$ =（+ $\sqrt{3}$ ）²；

(3)、若 $a + 4 \sqrt{3} = {(m + \sqrt{3} n)}^{2}$ ，且 $a ， b ， m ， n$ 均为正整数，求 $a$ 的值.

查看试题解析
24. 如图1， $△ A B C$ 的边 $B C$ 在直线 $l$ 上， $A C ⊥ B C$ ，且 $A C = B C$ ， $△ E F P$ 的边 $F P$ 也在直线 $l$ 上，边 $E F$ 与 $A C$ 重合，且 $E F = F P$ .

(1)、在图1中请你通过观察，猜想并直接写出 $A B$ 与 $A P$ 所满足的数量关系和位置关系；

(2)、将 $△ E F P$ 沿直线 $l$ 向左平移到图2的位置时， $E P$ 交 $A C$ 于点Q，连接AP，BQ，猜想并写出BQ与AP所满足的数量关系和位置关系，请证明你的猜想；

(3)、将△EFP沿直线l向左平移到图3的位置时，EP的延长线交AC的延长线于点Q，连接AP，BQ，你认为（2）中所猜想的BQ与AP的数量关系和位置关系还成立吗？若成立，给出证明；若不成立，请说明理由.

查看试题解析