重庆市渝中区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 三角形的三个外角的和是（　　）

A、90° B、180° C、270° D、360°

查看试题解析
2. 若（x﹣1）⁰＝1，则x的取值范围是（　　）

A、x≠0 B、x≠1 C、x≠﹣1 D、x＞1

查看试题解析
3. 用数学的眼光观察下面的网络图标，其中可以抽象成轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
4. 下列计算正确的是（　　）

A、x²+x＝x³ B、x²•x＝x³ C、（x²）³＝x⁵ D、（2x）³＝6x³

查看试题解析
5. 下列约分正确的是（　　）

A、 $\frac{x^{6}}{x^{2}}$ ＝x³ B、 $\frac{x + 1}{x + 1}$ ＝0 C、 $\frac{x^{2} + y^{2}}{x + y}$ ＝x+y D、 $\frac{x^{2} - y^{2}}{x + y}$ ＝x﹣y

查看试题解析
6. 一个多边形的内角和是外角和的4倍，则这个多边形的边数是（）

A、8 B、9 C、10 D、11

查看试题解析
7. 下列说法错误的是（　　）

A、有两边相等的三角形是等腰三角形 B、直角三角形不可能是等腰三角形 C、有两个角为60°的三角形是等边三角形 D、有一个角为60°的等腰三角形是等边三角形

查看试题解析
8. 下列各式从左到右的变形中，属于因式分解的是（　　）

A、a（a+1）＝a²+a B、a²+2a﹣1＝a（a+2）﹣1 C、4a²﹣2a＝2a（2a﹣1） D、a²﹣4+4a＝（a+2）（a﹣2）+4a

查看试题解析
9. 如图，在△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，若∠A＝30°，BD＝1，则AD的长为（　　）

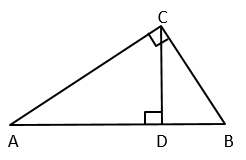A、 $\sqrt{3}$ B、2 C、3 D、2 $\sqrt{3}$

查看试题解析
10. 如图，有一张四边形纸片ABCD，AD∥BC，将它沿GH折叠，使点D落在AB边上的点E处，点C落在点Q处，若∠GHB＝80°，则∠AGE的度数为（　　）

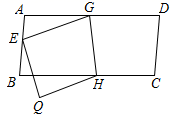A、20° B、30° C、35° D、40°

查看试题解析
11. 已知一个三角形三边的长分别为5，7，a，且关于y的分式方程 $\frac{y + 4 a}{y - 3} + \frac{5 a}{3 - y} = 2$ 的解是非负数，则符合条件的所有整数a的和为（　　）

A、24 B、15 C、12 D、7

查看试题解析
12. 现在汽车已成为人们出行的交通工具.李刚、王勇元旦那天相约一起到某加油站加油，当天95号汽油的单价为m元/升，他俩加油的情况如图所示.半个月后的某天，他俩再次相约到同一加油站加油，此时95号汽油的单价下调为n元/升，他俩加油的情况与上次相同，请运用所学的数学知识计算李刚、王勇两次加油谁的平均单价更低？低多少？下列结论正确的是（　　）

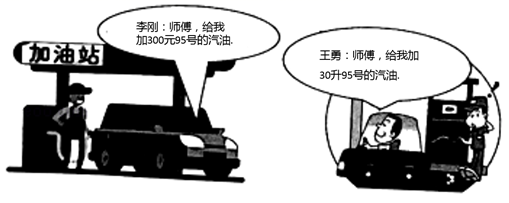A、李刚比王勇低 $\frac{{(m - n)}^{2}}{2 m n}$ 元/升 B、王勇比李刚低 $\frac{2 m n}{{(m - n)}^{2}}$ 元/升 C、王勇比李刚低 $\frac{{(m - n)}^{2}}{2 m n}$ 元/升 D、李刚与王勇的平均单价都是 $\frac{m + n}{2}$ 元/升

查看试题解析

二、填空题

13. 计算：（﹣2ab²）•（﹣3a²）＝.

查看试题解析
14. 人类进入5G时代，科技竞争日趋激烈.据报道，我国某种芯片的制作工艺已达到28纳米，居世界前列.已知1纳米＝1×10^﹣9米，则28纳米等于多少米？将其结果用科学记数法表示为.

查看试题解析
15. 将一副直角三角板如图放置，使两直角重合，则∠1=°.

查看试题解析
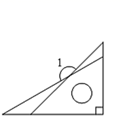16. 分解因式：x²（a﹣b）﹣a+b＝.

查看试题解析
17. 全民齐心协力共建共享文明城区建设.某服装加工厂计划为环卫工人生产1200套冬季工作服，在加工完480套后，工厂引进了新设备，结果工作效率比原计划提高了20%，结果共用54天完成了全部生产任务.若设该加工厂原计划每天加工x套冬季工作服，则根据题意列方程为.

查看试题解析
18. 如图，已知∠ABC、∠EAC的角平分线BP、AP相交于点P，PM⊥BE，PN⊥BF，垂足分别为M、N.现有四个结论：
①CP平分∠ACF；②∠BPC＝ $\frac{1}{2}$ ∠BAC；③∠APC＝90°﹣ $\frac{1}{2}$ ∠ABC；④S_△APM+S_△CPN＞S_△APC.

其中结论正确的为.（填写结论的编号）

查看试题解析

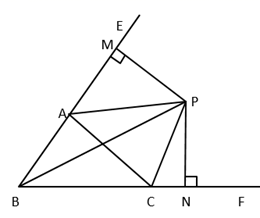
三、解答题

19. 计算：

(1)、（2a+b）（a﹣b）；

(2)、 $\frac{3 a b^{2}}{4 c} \div (- \frac{9 a^{2} b}{c^{3}}) \cdot {(\frac{c}{2 b})}^{- 2}$ .

查看试题解析
20. 解下列方程：

(1)、（x﹣1）²﹣x²＝3（x﹣3）；

(2)、 $\frac{x - 1}{x - 2} = \frac{2 x + 1}{x^{2} - 4} - 1$ .

查看试题解析
21. 如图，在△ABC中，AC＝BC，AD⊥BC，BE⊥AC，垂足分别为D、E.

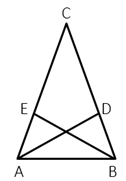
求证：

(1)、△ADC≌△BEC；

(2)、∠DAB＝∠EBA.

查看试题解析
22. 尺规作图：已知等腰三角形底边长为a，底边上的高的长为h，如图所示.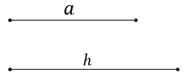

（ 1 ）求作这个等腰三角形；

（ 2 ）求作这个等腰三角形的一个底角的平分线.

要求：保留作图的痕迹，写出结论，但不要求写出作法.

查看试题解析
23.

(1)、先化简 $2 - \frac{2 a - 4}{a^{2} - 9} \div \frac{a - 2}{a^{2} + 6 a + 9} + \frac{6}{a - 3}$ ，再解答下列问题：

(2)、当a＝2021⁰时，求原式的值；

(3)、若原式的值是正整数，则求出对应的a的值.

查看试题解析
24. 阅读理解：
已知：a，b，c，d都是不为0的数，且 $\frac{a}{b} = \frac{c}{d}$ ，求证： $\frac{a + b}{b} = \frac{c + d}{d}$ .

证明：∵ $\frac{a}{b} = \frac{c}{d}$ ，

∴ $\frac{a}{b} + 1 = \frac{c}{d} + 1$ .

∴ $\frac{a + b}{b} = \frac{c + d}{d}$ .

根据以上方法，解答下列问题：

(1)、若 $\frac{a}{b} = \frac{3}{5}$ ，求 $\frac{a + b}{b}$ 的值；

(2)、若 $\frac{a}{b} = \frac{c}{d}$ ，且a≠b，c≠d，证明 $\frac{a - b}{a + b} = \frac{c - d}{c + d}$ .

查看试题解析
25. 为预防新冠疫情的反弹，康源药店派采购员到厂家去购买了一批A、B两种品牌的医用外科口罩.已知每个B品牌口罩的进价比A品牌口罩的进价多0.7元，采购员用7200元购进A品牌口罩的数量为用5000元购进B品牌数量的2倍.

(1)、求A、B两种品牌每个口罩的进价分别为多少元？

(2)、若B品牌口罩的售价是A品牌口罩的售价的1.5倍，要使康源药店销售这批A、B两种品牌口罩的利润为8800元，则它们的售价分别定为多少元？

查看试题解析
26. 在△ABC中，AB＝AC，D是BC边的中点，E、F分别是AD、AC边上的点.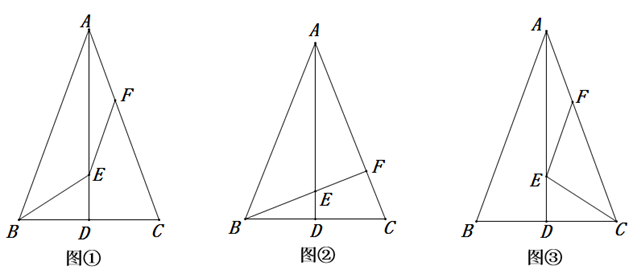

∴ $B E = E F$ ；

(1)、如图①，连接BE、EF，若∠ABE＝∠EFC，求证：BE＝EF；

(2)、如图②，若B、E、F在一条直线上，且∠ABE＝∠BAC＝45°，探究BD与AE的数量之间有何等量关系，并证明你的结论；

(3)、如图③，若AB＝13，BC＝10，AD＝12，连接EC、EF，直接写出EC+EF的最小值.

查看试题解析