重庆市梁平区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $- 2, 3.14, \sqrt{2}, \sqrt{4}$ 这4个数中，无理数是（）

A、 $- 2$ B、 $3.14$ C、 $\sqrt{2}$ D、 $\sqrt{4}$

查看试题解析
2. 下列运算正确的是（）

A、a⁶÷a³＝a² B、（a²）³＝a⁵ C、（﹣2a²）³＝﹣8a⁶ D、（2a＋1）²＝4a²＋2a＋1

查看试题解析
3. 下列各组线段能构成直角三角形的一组是（）

A、5，12，13 B、20，30，40 C、5，9，12 D、3，4，6

查看试题解析
4. 某商品四天内每天每斤的进价与售价信息如图所示，则售出这种商品每斤利润最大的是（）

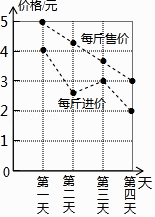A、第一天 B、第二天 C、第三天 D、第四天

查看试题解析
5. 如图，在△ABC和△DEF中，已有条件AB=DE，还需要添加两个条件才能使△ABC≌△DEF，不能添加的一组条件是（）

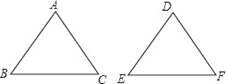A、∠B=∠E，BC=EF B、∠A=∠D，BC=EF C、∠A=∠D，∠B=∠E D、BC=EF，AC=DF

查看试题解析
6. 有40个数据，共分成6组，第1~4组的频数分别为10、5、7、6，第5组的频率是0. 1，则第6组的频率是（）

A、0. 2 B、0. 3 C、0. 1 D、0. 4

查看试题解析
7. 将一个含30°角的直角三角板ABC与一个直尺如图放置，∠ACB＝90°，点A在直尺边MN上，点B在直尺边PQ上，BC交MN于点D，若∠ABP＝15°，AC＝8，则AD的长为（　　）

A、 $\frac{15 \sqrt{2}}{2}$ B、8 C、8 $\sqrt{2}$ D、8 $\sqrt{3}$

查看试题解析
8. （ $\frac{2}{3}$ ）²⁰¹⁷×1.5²⁰¹⁶×（﹣1）²⁰¹⁷计算的结果是（）

A、 $\frac{2}{3}$ B、 $\frac{3}{2}$ C、﹣ $\frac{2}{3}$ D、﹣ $\frac{3}{2}$

查看试题解析
9. 等腰三角形 $A B C$ 中， $A B = A C$ ，一边上的中线 $B D$ 将这个三角形的周长分为 $15$ 和 $12$ 两部分，则这个等腰三角形的底边长为（）

A、7 B、7或11 C、11 D、7或10

查看试题解析
10. 下列命题中真命题的个数（）
（ 1 ）面积相等的两个三角形全等

（ 2 ）无理数包含正无理数、零和负无理数

（ 3 ）在直角三角形中，两条直角边长为n²﹣1和2n，则斜边长为n²＋1；

（ 4 ）等腰三角形面积为12，底边上的高为4，则腰长为5.

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 已知a＝2018x＋2018，b＝2018x＋2019，c＝2018x＋2020，则a²＋b²＋c²－ab－ac－bc的值是( )

A、0 B、1 C、2 D、3

查看试题解析
12. 如图所示，OA平分∠NOP，OB平分∠MOP，AB⊥OP于点E，BC⊥MN于点C，AD⊥MN于点D，下列结论错误的是（）

A、AD＋BC＝AB B、∠CBO＝∠BAO C、∠AOB＝90° D、点O是CD的中点

查看试题解析

二、填空题

13. 命题“如果m是整数，那么m一定是有理数”；则它的逆命题是命题（填写“真”或“假”）.

查看试题解析
14. 2019新型冠状病毒（2019﹣mCoV），2020年1月12日被世界卫生组织命名.科学家借助比光学显微镜更加厉害的电子显微镜发现新型冠状病毒的大小约为0.000000215米.则数据0.000000215用科学记数法表示为.

查看试题解析
15. 一个长方形的面积为 $12 x^{2} - 3 x$ ，它的宽为 $3 x$ ，用代数式表示它的长为．

查看试题解析
16. 如图，△ACE≌△DBF，如果∠E＝∠F，DA＝12，CB＝2，那么线段AB的长是．

查看试题解析
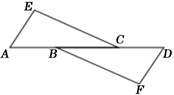17. 对于非零的两个实数a，b，规定a⊗b＝a³﹣ab，那么将a⊗16进行分解因式的结果为.

查看试题解析
18. 如图，AO⊥OM，OA=7，点B为射线OM上的一个动点，分别以OB，AB为直角边，B为直角顶点，在OM两侧作等腰Rt△OBF、等腰Rt△ABE，连接EF交OM于P点，当点B在射线OM上移动时，则PB的长度.

查看试题解析

三、解答题

19. 计算下列各题：

(1)、﹣1²⁰²⁰＋（ $\frac{1}{2}$ ）^﹣2﹣|﹣3|＋（4﹣5.67）⁰；

(2)、 $999^{2}$ ﹣1002×998.

查看试题解析
20. 先化简，再求值：

(1)、6x²y（﹣2xy＋y³）÷xy² ，其中x＝2，y＝﹣1；

(2)、（x＋2y）（x﹣2y）＋（x﹣2y）²﹣（6x²y﹣2xy²）÷（2y），其中x＝﹣2，y＝ $\frac{1}{2}$ .

查看试题解析
21. 在大课间活动中，同学们积极参加体育锻炼，小明在全校随机抽取一部分同学就“我最喜体育项目”进行了一次抽样调查.如图是他通过收集的数据绘制的两幅不完整的统计图，请你根据图中提供的信息，解答下列问题：

(1)、小明共抽取名学生；

(2)、补全条形统计图并填写扇形统计图中的百分比；

(3)、若全校共有2130人，请你估算“其他”部分的学生人数.

查看试题解析
22. 如图，方格中小正方形的边长为1，△ABC的三个顶点都在小正方形的格点上，求：

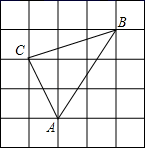(1)、△ABC的周长；

(2)、请判断三角形ABC是否是直角三角形，并说明理由；

(3)、△ABC的面积；

(4)、点C到AB边的距离.

查看试题解析
23. 如图，已知∠ACB＝∠DCE＝90°，AC＝BC＝6，CD＝CE，AE＝3，∠CAE＝45°，

(1)、求证△ACD≌△BCE；

(2)、求AD的长.

查看试题解析
24. 证明：如果两个三角形有两条边和其中一边上的中线分别相等，那么这两个三角形全等.按下列步骤证明上述命题（根据所画图形，用符号表示已知和求证，并写出证明过程）：
已知：

求证：

证明：

查看试题解析
25. 观察“探究性学习”小组的甲、乙两名同学进行的分解因式：
甲：x²＋2ax﹣3a²

＝x²＋2ax＋a²﹣a²﹣3a²

＝（x＋a）²﹣4a²（分成两组）

＝（x＋a）²﹣（2a）²

＝（x＋3a）（x﹣a）（平方差公式）；

乙：a²﹣b²﹣c²＋2bc

＝a²﹣（b²＋c²﹣2bc）（分成两组）

＝a²﹣（b﹣c）²（直接运用公式）

＝（a＋b﹣c）（a﹣b＋c）（再用平方差公式）

请你在他们解法的启发下，把下列各式分解因式：

(1)、x²﹣4x＋3；

(2)、x²﹣2xy﹣9＋y².

查看试题解析
26. 如图，在△ABC中，点D为BC边上的一点，AB＝AD，点E为AC上的一点，△CDE为等边三角形，过点D作DF⊥AC于点F.

(1)、若AB＝6，CD＝2，求AE的长；

(2)、点G为AE上的一点，连接BG、BE，若BE＝BG，求证：AG＝EF＋ $\sqrt{3}$ DF.

查看试题解析