重庆市九龙坡区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 如果分式 $\frac{2}{x - 1}$ 有意义，那么x的取值范围是（）

A、 $x = 1$ B、 $x \neq 0$ C、 $x \neq 1$ D、 $x \geq 1$

查看试题解析
2. 下列图案属于轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 计算 ${(a^{2} b)}^{3}$ 的结果是（）

A、 $a^{6}$ B、 $a^{2} b^{3}$ C、 $a^{5} b^{3}$ D、 $a^{6} b^{3}$

查看试题解析
4. 观察下列图形，图（1）中有3个三角形，图（2）中有5个三角形，图（3）中有7个三角形，…若依此规律下去，则第5个图形中三角形的个数是（　　）

A、9个 B、11个 C、13个 D、15个

查看试题解析
5. 如果等腰三角形的两边长分别为7cm和3cm.那么它的第三边的长是（）

A、3cm B、4cm C、7cm D、3cm或7cm

查看试题解析
6. 在下列运算中，正确的是（）

A、（x﹣y）²＝x²﹣y² B、（a+2）（a﹣3）＝a²﹣6 C、（a+2b）²＝a²+4ab+4b² D、（2x﹣y）（2x+y）＝2x²﹣y²

查看试题解析
7. 如图，已知点A，D，C，F在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需要添加一个条件是（）

A、∠BCA=∠F B、∠B=∠E C、BC∥EF D、∠A=∠EDF

查看试题解析
8. 如图，在△ABC中，∠ABC=50°，∠BAC=20°，D为线段AB的垂直平分线与直线BC的交点，连结AD，则∠CAD=（）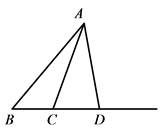

A、40° B、30° C、20° D、10°

查看试题解析
9. A，B两地相距48千米，一艘轮船从A地顺流航行至B地，又立即从B地逆流返回A地，共用去9小时，已知水流速度为4千米/时，若设该轮船在静水中的速度为x千米/时，则可列方程（）

A、 $\frac{48}{x + 4} + \frac{48}{x - 4} = 9$ B、 $\frac{48}{4 + x} + \frac{48}{4 - x} = 9$ C、 $\frac{48}{x}$ +4=9 D、 $\frac{96}{x + 4} + \frac{96}{x - 4} = 9$

查看试题解析
10. 数学课上，老师提出如下问题：
如图1，点P、Q是直线l同侧的两点，请你在直线l上确定一个点R.使 $△ P Q R$ 的周长最小.小明的作法如下，如图2：

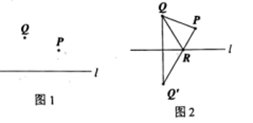
（ 1 ）作点Q关于直线l的对称点 $Q^{'}$ ；

（ 2 ）连接 $P Q^{'}$ ，交直线l于点R；

（ 3 ）连接RQ、PQ.

那么点R就是使 $△ P Q R$ 的周长最小的点.

老师说，小明的做法正确.接着.老师问同学们，小明这种作法应用了哪些我们学过的定理呢？有四位同学分别说了一个定理，下面的A，B，C，D四个答案分别代表了四个同学所说的定理，其中小明没有应用到的定理是（）

A、如果两个图形关于某直线对称，那么对称轴是对称点连线的垂直平分线 B、等腰三角形底边上的高也是顶角的角平分线 C、线段垂直平分线上的点到线段两个端点的距离相等 D、两点之间，线段最短

查看试题解析
11. 若关于x的分式方程 $\frac{x}{x - 2} = 2 - \frac{m}{2 - x}$ 有非负整数解，且关于y的不等式组 ${\begin{array}{l} \frac{y}{2} + 1 \geq \frac{y + 2}{3} \\ 5 (y - 1) < y - (m + 3) \end{array}$ 有且只有2个整数解，则所有符合条件的正整数m的和为（）

A、5 B、7 C、8 D、9

查看试题解析
12. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，D是 $A B$ 上的点，过点D作 $D E ⊥ A B$ 交 $B C$ 于点F，交 $A C$ 的延长线于点E，连接 $C D$ ， $∠ D C A = ∠ D A C$ .下列结论：① $∠ D C B = ∠ B$ ：② $C D = \frac{1}{2} A B$ ③ $△ A D C$ 是等边三角形：④若 $∠ E = 30 °$ ，则 $D E = E F + C F$ .其中正确的是（　　）

A、①②③ B、①③④ C、①②④ D、②③④

查看试题解析

二、填空题

13. 计算 ${(π - 3)}^{0} - 2^{3} =$ .

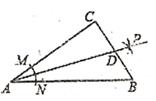
查看试题解析
14. 若一个多边形的内角和是其外角和的3倍，则这个多边形的边数是．

查看试题解析
15. 约分： $\frac{x^{2} - 9}{4 x^{2} - 12 x} =$ .

查看试题解析
16. 如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M、N，再分别以点M、N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，作射线AP，交边BC于点D若CD=4，AB=15，则△ABD的面积是。

查看试题解析
17. 在平面直角坐标系中，已知点A（1，2），B（5，5），C（5，2），存在点E，使△ACE和△ACB全等，写出所有满足条件的E点的坐标．

查看试题解析
18. 如图所示，在等边三角形ABC中，AB边上的高 $C D = 15$ ，E是CD上一点，现有一动点Р沿着折线 $B - E - C$ 运动，在BE上的速度是每秒3个单位长度.在CE上的速度是每秒6个单位长度.则点Р从B到C的运动过程中最少需秒.

查看试题解析

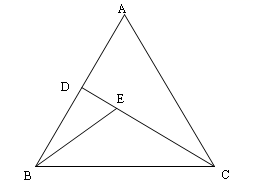
三、解答题

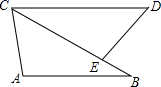
19. 已知：如图，E是BC上一点，AB＝EC，AB∥CD，BC＝CD.求证：AC＝ED.

查看试题解析
20.

(1)、因式分解： $x^{3} + 2 x^{2} y + x y^{2}$ ；

(2)、解方程： $\frac{1}{x + 3} - \frac{2}{3 - x} = \frac{12}{x^{2} - 9}$

查看试题解析
21. 化简：

(1)、（2a﹣b）²+（a+b）（a﹣b）

(2)、（ $\frac{5 a + 4}{a - 1} +$ a） $\div \frac{a^{2} - 4}{a - 1}$

查看试题解析
22. 如图，在等腰 $Δ A B C$ 中， $A C = B C$ ， $∠ A C B = 4 ∠ B$ ，点D是 $A C$ 边的中点， $D E ⊥ A C$ 交 $A B$ 于点E，连接 $C E$ .

(1)、求 $∠ B C E$ 的度数：

(2)、求证： $A B = 3 C E$ .

查看试题解析
23. 某书店老板去图书批发市场购买某种图书.第一次用1200元购书若干本，并按该书的定价7元出售，很快售完.由于该书畅销，第二次购书时，每本书的批发价已比第一次提高了20%，他用1500元所购该书数量比第一次多10本，并按该书的定价7元售出200本时，出现滞销，便以定价的4折售完剩余的书.

(1)、第一次购书的批发价为每本多少元？

(2)、该老板这两次售书总体上是赔钱了，还是赚钱了（不考虑其它因素）？若赔钱，赔多少？若赚钱，赚多少？

查看试题解析
24. 如图1是一个长为4a、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成的一个“回形”正方形（如图2）.

(1)、图2中的阴影部分的面积为；

(2)、观察图2请你写出（a+b）²、（a-b）²、ab之间的等量关系是；

(3)、根据（2）中的结论，若x+y=7，xy= $\frac{45}{4}$ ，则x-y= ；

(4)、实际上通过计算图形的面积可以探求相应的等式.根据图3，写出一个因式分解的等式 .

查看试题解析
25. 如图，等腰直角三角形ABC中， $A B = A C$ ， $∠ B A C = 90 °$ .

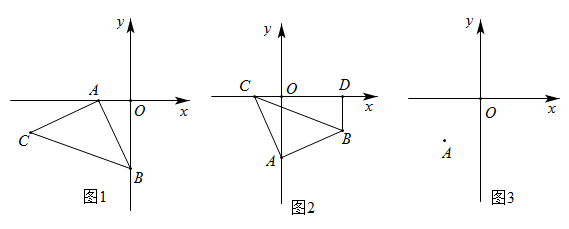(1)、如图1，等腰直角三角形ABC的顶点A在x轴的负半轴上，点B在y轴的负半轴上，且 $O A = 2$ ， $O B = 4$ ，求点C的坐标；

(2)、如图2，等腰直角三角形ABC顶点A在y轴的负半轴上，点C在x轴的负半轴上，过点B作 $B D ⊥ x$ 轴于点D，求证： $O A - O C = B D$ ；

(3)、如图3，点A的坐标为 $(- 3 ， - 3)$ ，点 $B (0 ， m)$ 在y轴上运动，点 $C (n ， 0)$ 在x轴上运动，在点B、C 的运动过程中，能否使得 $△ A B C$ 是一个以点A为直角顶点的等腰直角三角形，如果存在，请你直接写出m和n的数量关系；如果不存在，请说明理由.

查看试题解析
26. 在△ABC中，AB=AC，点D是直线BC上一点（不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE =∠BAC，连接CE.

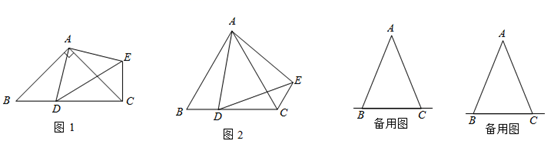(1)、如图1，当点D在线段BC上，如果∠BAC=90°，则∠BCE=度；

(2)、设 $∠ B A C = α$ ， $∠ B C E = β$ .
①如图2，当点在线段BC上移动，则 $α$ ， $β$ 之间有怎样的数量关系？请说明理由；

②当点在直线BC上移动，则 $α$ ， $β$ 之间有怎样的数量关系？请直接写出你的结论.

查看试题解析