浙江省温州市瑞安市2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列选项中的图标，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各组数可能是一个三角形的边长的是（）

A、1，2，6 B、2，3，4 C、4，4，8 D、5，6，12

查看试题解析
3. 在平面直角坐标系中，点 $A (- 4, 5)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 若 $m > n$ ，则下列各式中错误的是（）

A、 $m + 2 > n + 2$ B、 $m - 3 > n - 3$ C、 $- 3 m > - 3 n$ D、 $\frac{m}{2} > \frac{n}{2}$

查看试题解析
5. 能说明命题“对于任何实数a，都有 $a^{2} > a$ ”是假命题的反例是（）

A、 $a = - 1$ B、 $a = 0$ C、 $a = 2$ D、 $a = 3$

查看试题解析
6. 已知点 $(- 2, y_{1})$ ， $(0, y_{2})$ ， $(4, y_{3})$ 是直线 $y = - 5 x + b$ 上的三个点，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）.

A、 $y_{1} > y_{2} > y_{3}$ B、 $y_{1} < y_{2} < y_{3}$ C、 $y_{1} > y_{3} > y_{2}$ D、 $y_{1} < y_{3} < y_{2}$

查看试题解析
7. 如图，在四边形 $A B C D$ 中， $B D$ 平分 $∠ A B C$ ， $A D // B C$ ， $∠ C = 90 °$ ， $A B = 5$ ， $C D = 4$ ，则四边形 $A B C D$ 的周长是（）.

A、18 B、20 C、22 D、24

查看试题解析
8. 如图， $A B = D E$ ， $∠ A = ∠ D$ ，要说明 $△ A B C ≌ △ D E F$ ，需添加的条件不能是（）

A、 $A B // D E$ B、 $A C // D F$ C、 $A C ⊥ D E$ D、 $A C = D F$

查看试题解析
9. 一次函数 $y = k x + b$ 中x与y的部分对应值如下表，则不等式 $k x + b > 0$ 的解是（）

x

-2

-1

0

1

y

5

3

1

-1

A、 $x > 0$ B、 $x < 1$ C、 $x > 0.5$ D、 $x < 0.5$

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ，以 $△ A B C$ 的各边为边分别作正方形 $B A H I$ ，正方形 $B C F G$ 与正方形 $C A D E$ .延长 $B G$ ， $F G$ 分别交 $A D$ ， $D E$ 于点K，J，连结 $D H$ ， $I J$ .图中两块阴影部分面积分别记为 $S_{1}$ ， $S_{2}$ ，若 $S_{1} ： S_{2} = 1 ： 4$ ，四边形 $S_{B A H E} = 18$ ，则四边形 $M B N J$ 的面积为（）

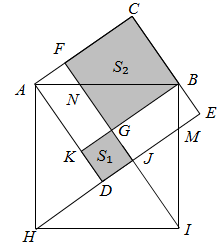A、5 B、6 C、8 D、9

查看试题解析

二、填空题

11. 若m与3的和小于m的2倍，则可列出不等式：.

查看试题解析
12. 若点 $A (3, m)$ 关于x轴的对称点坐标为 $(3, - 5)$ ，则 $m =$ .

查看试题解析
13. 在 $Rt △ A B C$ 中， $∠ A B C = 90 °$ ，D为斜边 $A C$ 中点， $A C = 8$ ，则 $B D =$ .

查看试题解析
14. △ABC中，AB=AC，∠B=70°，则∠A的度数是.

查看试题解析
15. 一条笔直的公路上依次有A，B，C三地，甲，乙两人同时从A地出发，甲先使用共享单车，经过B地到达停车点C地后再步行返回B地，此时直接步行的乙也恰好到达B地.已知两人步行速度相同，两人离起点A的距离y（米）关于时间x（分）的函数关系如图，则 $m =$ .

查看试题解析
16. 如图1，塔吊是建筑工地上常用的一种起重设备，可以用来搬运货物.如图2，已知一款塔吊的平衡臂 $A B C$ 部分构成一个直角三角形，且 $A C = B C$ ，起重臂 $A D$ 可以通过拉伸 $B D$ 进行上下调整.现将起重臂 $A D$ 从水平位置调整至 $A D_{1}$ 位置，使货物E到达 $E_{1}$ 位置（挂绳 $D E$ 的长度不变且始终与地面垂直）.此时货物E升高了24米，且到塔身 $A H$ 的距离缩短了16米，测得 $A B ⊥ B D_{1}$ ，则 $A C$ 的长为米.

查看试题解析

三、解答题

17. 解不等式组： ${\begin{array}{l} x + 3 \leq 4 \\ 2 (x - 1) > - 8 \end{array}$ ，并把解表示在数轴上.

查看试题解析
18. 如图， $A B = A C$ ， $A D = A E$ ， $∠ B A D = ∠ C A E$ ，求证： $∠ D = ∠ E$ .

查看试题解析
19. 已知点A在直角坐标系中的位置如图.

(1)、点A的坐标为，点A与点O之间的距离为.

(2)、在图中画一个等腰三角形 $A P Q$ ，使点P，Q分别落在x轴，y轴上，且各顶点的横，纵坐标都是整数.

查看试题解析
20. 如图，直线 $y = k x + b$ 分别交x轴于点 $A (4 ， 0)$ ，交y轴于点 $B (0 ， 8)$ .

(1)、求直线 $A B$ 的函数表达式.

(2)、若点 $P (2 ， m)$ ，点 $Q (n ， 2)$ 是直线 $A B$ 上两点，求线段 $P Q$ 的长.

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $∠ B = 90 °$ ， $A C$ 平分 $∠ B A D$ ， $D E ⊥ A C$ ， $A B = A E$ .

(1)、求证： $A C = A D$ .

(2)、若 $B C ⊥ C D$ ，试判断 $△ A C D$ 的形状，并说明理由.

查看试题解析

22. 某校组织元旦汇演，准备购进A，B两种文具共40件作为奖品，设购进A种文具x件，总费用为y元.A，B文具的费用与x的函数关系如下表.

x（件）	8	9	12
A种文具费用（元）	120	135	______
B种文具费用（元）	640	______	560

(1)、将表格补充完整.

(2)、求y关于x的函数表达式.

(3)、当A种文具的费用不大于B种文具的费用时，求总费用y的最小值.

查看试题解析

23. 如图，直线 $y = - x + 4$ 交y轴于点A，交x轴于点B，直线 $y = - 0.5 x + 2.5$ 交y轴于点C，交直线 $A B$ 于点D，点P为线段 $C D$ 上一点，作 $P M ⊥ x$ 轴， $P N ⊥ y$ 轴，延长 $N P$ 交直线 $A B$ 于点Q，记 $O M = m$ ， $P Q = n$ .

(1)、求点D的坐标.

(2)、求n关于m的函数关系式.

(3)、记点P关于直线 $A B$ 对称点 $P^{'}$ ，连结 $N P^{'}$ ， $D P^{'}$ ， $N D$ .
①当 $△ N D P^{'}$ 为等腰三角形时，求n的值.

②记直线 $P P^{'}$ 交y轴于点E，若 $O N \geq 2 O E$ ，则m的取值范围为.

查看试题解析