四川省内江市2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 下列说法正确的是( )A、4的平方根是2 B、 的平方根是±4 C、-36的算术平方根是6 D、25的平方根是±52. 下列计算中正确的是( ).A、 B、 C、 D、3. 如图,AB//DE,AC//DF,AC=DF,下列条件中,不能判定△ABC≌△DEF的是( )
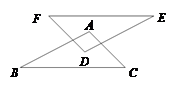 A、AB=DE B、∠B=∠E C、EF=BC D、EF//BC4. 如图,已知 ,以点O为圆心,任意长度为半径画弧①,分别交 于点 ,再以点E为圆心, 的长为半径画弧,交弧①于点D,画射线 .若 ,则 的度数为( )
A、AB=DE B、∠B=∠E C、EF=BC D、EF//BC4. 如图,已知 ,以点O为圆心,任意长度为半径画弧①,分别交 于点 ,再以点E为圆心, 的长为半径画弧,交弧①于点D,画射线 .若 ,则 的度数为( ) A、 B、 C、 D、5. 一个长方形的面积为 ,且一边长为 ,则另一边的长为( )A、 B、 C、 D、6. 初二(1)班有48位学生,春游前,班长把全班学生对春游地点的意向绘制成了扇形统计图,其中“想去苏州乐园的学生数”的扇形圆心角60°,则下列说法正确的是( )A、想去苏州乐园的学生占全班学生的60% B、想去苏州乐园的学生有12人 C、想去苏州乐园的学生肯定最多 D、想去苏州乐园的学生占全班学生的1/67. 下列命题正确的是( )A、等腰三角形的角平分线、中线、高线互相重合 B、在角的内部,到角两边距离相等的点在这个角的平分线上 C、有一个角是60°的三角形是等边三角形 D、有两边及一边的对角对应相等的两个三角形全等8. 已知x,y,z是正整数,x y,且 ,则 等于( )A、 B、1或23 C、1 D、 或9. 如图, 是 的角平分线, ,垂足为E, , , ,则 长为( )
A、 B、 C、 D、5. 一个长方形的面积为 ,且一边长为 ,则另一边的长为( )A、 B、 C、 D、6. 初二(1)班有48位学生,春游前,班长把全班学生对春游地点的意向绘制成了扇形统计图,其中“想去苏州乐园的学生数”的扇形圆心角60°,则下列说法正确的是( )A、想去苏州乐园的学生占全班学生的60% B、想去苏州乐园的学生有12人 C、想去苏州乐园的学生肯定最多 D、想去苏州乐园的学生占全班学生的1/67. 下列命题正确的是( )A、等腰三角形的角平分线、中线、高线互相重合 B、在角的内部,到角两边距离相等的点在这个角的平分线上 C、有一个角是60°的三角形是等边三角形 D、有两边及一边的对角对应相等的两个三角形全等8. 已知x,y,z是正整数,x y,且 ,则 等于( )A、 B、1或23 C、1 D、 或9. 如图, 是 的角平分线, ,垂足为E, , , ,则 长为( ) A、 B、 C、 D、10. 如图1,已知 AB=AC,D为∠BAC 的平分线上一点,连接 BD、 CD;如图2,已知 AB= AC,D、E为∠BAC的平分线上两点,连接 BD,CD,BE,CE;如图3,已知 AB=AC,D,E,F为∠BAC的平分线上三点,连接BD,CD,BE,CE, BF,CF;…,依次规律,第 n个图形中全等三角形的对数是( )
A、 B、 C、 D、10. 如图1,已知 AB=AC,D为∠BAC 的平分线上一点,连接 BD、 CD;如图2,已知 AB= AC,D、E为∠BAC的平分线上两点,连接 BD,CD,BE,CE;如图3,已知 AB=AC,D,E,F为∠BAC的平分线上三点,连接BD,CD,BE,CE, BF,CF;…,依次规律,第 n个图形中全等三角形的对数是( ) A、n B、2n-1 C、 D、3(n+1)11. 已知 , , ,则代数式 的值为( )A、0 B、1 C、2 D、312. 如图,在Rt△ABC中,∠BAC=90°,∠C=45°,AD⊥BC于点D,∠ABC 的平分线分别交 AC、AD于E、F 两点,M为EF 的中点,AM的延长线交 BC于点N,连接EN,下列结论:①△AFE为等腰三角形;②DF= DN;③AN = BF;④EN⊥NC.其中正确的结论有( )
A、n B、2n-1 C、 D、3(n+1)11. 已知 , , ,则代数式 的值为( )A、0 B、1 C、2 D、312. 如图,在Rt△ABC中,∠BAC=90°,∠C=45°,AD⊥BC于点D,∠ABC 的平分线分别交 AC、AD于E、F 两点,M为EF 的中点,AM的延长线交 BC于点N,连接EN,下列结论:①△AFE为等腰三角形;②DF= DN;③AN = BF;④EN⊥NC.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 计算: .14. 已知 是有理数,若 ,则 的所有值为.15. 有一列数 , , , , , ,则第 个数是.16. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,将边AC沿CE翻折,使点A落在AB上的点D处;再将边 BC沿CF翻折,使点B落在CD的延长线上的点B'处,两条折痕与斜边AB分别交于点 E、F,则△B'FC 的面积为.


三、解答题
-
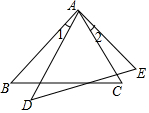
17.(1)、计算: .(2)、先化简,再求值: ,其中 , .18. 如图,在△ABC和△ADE中,AB=AD,∠B=∠D,∠1=∠2.
求证:BC=DE.
 19. 某校开展以“防疫有我,爱卫同行”为主题的线上活动、举办了A自制口罩,B防疫诗歌,C防疫故事,D防疫画报共四个项目的比赛,要求每位学生必须参加且仅参加一项,小丽随机调查了部分学生的报名情况,并绘制了下列两幅不完整的统计图.请根据统计图中信息解答下列问题:
19. 某校开展以“防疫有我,爱卫同行”为主题的线上活动、举办了A自制口罩,B防疫诗歌,C防疫故事,D防疫画报共四个项目的比赛,要求每位学生必须参加且仅参加一项,小丽随机调查了部分学生的报名情况,并绘制了下列两幅不完整的统计图.请根据统计图中信息解答下列问题: (1)、本次调查的学生总人数是人,扇形统计图中“D”部分的圆心角度数度.(2)、请将条形统计图补充完整.(3)、若全校共有 名学生,请估计该校报名参加防疫故事和防疫画报比赛的学生共有多少人?20. 如图, 中, 的垂直平分线 分别交 , 于点D,E,且 .
(1)、本次调查的学生总人数是人,扇形统计图中“D”部分的圆心角度数度.(2)、请将条形统计图补充完整.(3)、若全校共有 名学生,请估计该校报名参加防疫故事和防疫画报比赛的学生共有多少人?20. 如图, 中, 的垂直平分线 分别交 , 于点D,E,且 .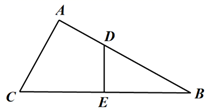
 (1)、求证: ;(2)、若 , ,求 的长.21. 把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.
(1)、求证: ;(2)、若 , ,求 的长.21. 把代数式通过配凑等手段,得到局部完全平方式,再进行有关运算和解题,这种解题方法叫做配方法.如:①用配方法分解因式:a2+6a+8,
解:原式=a2+6a+8+1-1=a2+6a+9-1
=(a+3)2-12=
②M=a2-2a-1,利用配方法求M的最小值.
解:
∵(a-b)2≥0,∴当a=1时,M有最小值-2.
请根据上述材料解决下列问题:
(1)、用配方法因式分解: .(2)、若 ,求M的最小值.(3)、已知x2+2y2+z2-2xy-2y-4z+5=0,求x+y+z的值.22. (1)、问题发现:如图1,已知C为线段AB上一点,分别以线段AC、BC为直角边作等腰直角三角形,∠ACD=90°,CA=CD,CB=CE,连接AE、BD,则AE、BD之间的数量关系为;位置关系为.(2)、拓展探究:如图2,把Rt△ACD绕点C逆时针旋转,线段AE、BD交于点F,则 AE与 BD 之间的关系是否仍然成立?请说明理由.(3)、拓展延伸:如图3,已知AC=CD,BC=CE,∠ACD=∠BCE=90°,连接AB、AE、AD,把线段 AB绕点A旋转,若AB=5,AC=3,请直接写出旋转过程中线段AE的最大值.
(1)、问题发现:如图1,已知C为线段AB上一点,分别以线段AC、BC为直角边作等腰直角三角形,∠ACD=90°,CA=CD,CB=CE,连接AE、BD,则AE、BD之间的数量关系为;位置关系为.(2)、拓展探究:如图2,把Rt△ACD绕点C逆时针旋转,线段AE、BD交于点F,则 AE与 BD 之间的关系是否仍然成立?请说明理由.(3)、拓展延伸:如图3,已知AC=CD,BC=CE,∠ACD=∠BCE=90°,连接AB、AE、AD,把线段 AB绕点A旋转,若AB=5,AC=3,请直接写出旋转过程中线段AE的最大值.