内蒙古包头市2019-2020学年高一下学期数学期末考试试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 与直线 关于坐标原点对称的直线方程为( )A、 B、 C、 D、2. 下列命题为真命题的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则3. 用斜二测画法画水平放置的平面图形直观图时,下列结论中正确的个数是( )
①平行的线段在直观图中仍然平行;②相等的线段在直观图中仍然相等;
③相等的角在直观图中仍然相等;④正方形在直观图中仍然是正方形
A、1 B、2 C、3 D、44. 点 在直线 上, 是坐标原点,则 的最小值是( )A、1 B、 C、2 D、5. 已知 为等比数列,下面结论中正确的是( )A、若 ,则 B、若 ,则 C、 D、6. 在△ 中, ,那么这个三角形的最大角是( )A、 B、 C、 D、7. 某几何体的三视图如图所示,该几何体由一平面将正方体截去一部分后所得,则截去几何体的体积与剩余几何体的体积比值为( )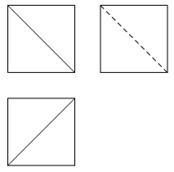 A、 B、 C、 D、8. 已知在正方体 中, 分别为 的中点,则异面直线 和 所成的角为( )A、 B、 C、 D、9. 已知点 , ,若直线 与线段 恒有公共点,则 的取值范围是( )A、 B、 C、 D、10. 已知 , ,则 的最小值为( )A、2 B、 C、 D、411. 《九章算术》中,将四个面都为直角三角形的三棱锥称为鳖臑.若三棱锥 为鳖臑, 平面 , , ,且三棱锥 的四个顶点都在一个正方体的顶点上,则该正方体的表面积为( )A、12 B、18 C、24 D、3612. 已知函数 满足 ,若数列 满足 ,则数列 的前10项和为( )A、 B、33 C、 D、34
A、 B、 C、 D、8. 已知在正方体 中, 分别为 的中点,则异面直线 和 所成的角为( )A、 B、 C、 D、9. 已知点 , ,若直线 与线段 恒有公共点,则 的取值范围是( )A、 B、 C、 D、10. 已知 , ,则 的最小值为( )A、2 B、 C、 D、411. 《九章算术》中,将四个面都为直角三角形的三棱锥称为鳖臑.若三棱锥 为鳖臑, 平面 , , ,且三棱锥 的四个顶点都在一个正方体的顶点上,则该正方体的表面积为( )A、12 B、18 C、24 D、3612. 已知函数 满足 ,若数列 满足 ,则数列 的前10项和为( )A、 B、33 C、 D、34二、填空题
-
13. 已知实数 , 满足 ,则 的最小值为.14. 若关于 的方程 没有实数根,则实数 的取值范围是.15. 《莱因德纸草书》(RhindPapyrus)是世界上最古老的数学著作之一.书中有这样一道题目:把100个面包分给5个人,使得每个人所得成等差数列,且较大的三份之和的 是较小的两份之和,则最大的1份为.16. 设三棱锥 的底面和侧面都是全等的正三角形, 是棱 的中点.记直线 与直线 所成角为 ,直线 与平面 所成角为 ,二面角 的平面角为 ,则 , , 中最大的是 , 最小的是.
三、解答题
-
17. 已知 , ,求证:(1)、 ;(2)、 .18. 已知 , , , 是第三象限角.(1)、求 的值;(2)、求 的值.19. △ 的内角 , , 的对边分别为 , , .已知 , , .(1)、求 ;(2)、求△ 的面积.