江苏省泰州医药高新技术产业开发区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期：2021-04-19 类型：期末考试
一、单选题
-
1. 下列图案中不是轴对称图形的是（ ）A、
B、
C、
D、
2. 已知：如图，∠1＝∠2，则不一定能使△ABD≌△ACD的条件是 （ ）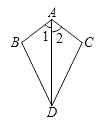
A、AB＝AC B、BD＝CD C、∠B＝∠C D、∠BDA＝∠CDA3. 下列各组数中是勾股数的是（ ）A、4，5， 6 B、1.5，2， 2.5 C、11，60， 61 D、1， ，24. 的整数部分是（ ）A、2 B、3 C、4 D、55. 点P（1，﹣2）关于x轴对称的点的坐标是（ ）A、（1，2） B、（﹣1，﹣2） C、（﹣1，2） D、（﹣2，1）6. 已知直线y=kx+b不经过第一象限，则下列结论正确的是（ ）A、k＞0，b＜0 B、k＜0，b＜0 C、k＜0，b≤0 D、k＜0，b≥0二、填空题
-
7. 在平面直角坐标系中，点A(2， )一定在第象限.8. 已知地球的半径约为6.4×103km，这个近似数精确度为km.9. 已知 ，则a的取值范围是.10. 若点A（x，5）与B（2，5）的距离为3，则x＝.11. 一次函数y=3x-1中，y随x的增大而.12. 如图， 中， ， 的平分线交BC于点D， 于点E， ，则 面积是.
13. 底角为45°的等腰三角形一边长为4cm，则此等腰三角形的底边长=cm.14. 如图，平面直角坐标系xOy中，直线y1＝k1x＋b1的图象与直线y2＝k2x＋b2的图象相交于点（－1，－3），当y1＜y2时，实数x的取值范围为.
15. 在平面直角坐标系xOy中，我们把横、纵坐标都是整数的点叫做整点.已知点A（0，4），点B（a，0）是x轴正半轴上的点，若△AOB内部（不包括边界）的整点个数为6，则 a的取值范围是.
三、解答题
-
16.(1)、计算： ；(2)、已知： ，求x的值.17. 已知y与x-2成正比例，且x＝1时，y＝2.(1)、求y与x之间的函数关系式；(2)、若点（a，-2）不在这个函数图象上，求a的取值范围.18. 如图，长7.5m的梯子靠在墙上，梯子的底部离墙的底端4.5m.
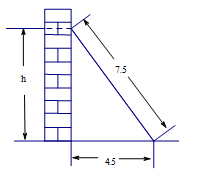(1)、求梯子的顶端到地面的距离；(2)、由于地面有水，梯子底部向右滑动1.5m，则梯子顶端向下滑多少米？19. 在平面直角坐标系xOy中，点A、B、C的坐标分别为（－1，0）、（－2，3）、（－3，1）.
(1)、写出△ABC的面积，S△ABC＝； △ABC形状是；(2)、在y轴上找一点D，使得BD＋DA的值最小，求D点的坐标.20. 如图，在△ABC中，AB=AC，D是BC的中点，DE⊥AB， DF⊥AC，E、F分别是垂足.
(1)、试说明：DE=DF；(2)、若AB=AC=13，BC=10，求DE.21. 某长途汽车客运公司规定旅客可以免费携带一定质量的行李，当行李的质量超过规定时，需付的行李费y(元)与行李质量x(kg)之间的函数表达式为 ，这个函数的图象如图所示，求：
(1)、k和b的值；(2)、旅客最多可免费携带行李的质量；(3)、行李费为4~15元时，旅客携带行李的质量为多少？22. 我们刚刚学习的勾股定理是一个基本的平面几何定理，也是数学中最重要的定理之一.勾股定理其实有很多种证明方法.下图是1876年美国总统伽菲尔德（Garfield）证明勾股定理所用的图形：以a、b为直角边，以c为斜边作两个全等的直角三角形，把这两个直角三角形拼成如图所示梯形形状，使C、B、D三点在一条直线上.
(1)、求证：∠ 90°；(2)、请你利用这个图形证明勾股定理（即证明： ）.23. 如图1，甲、乙两个容器内都装了一定数量的水，现将甲容器中的水匀速倒入乙容器中. 图2中，线段AB、线段CD分别表示容器中的水的深度h（厘米）与倒入时间t（分钟）的函数图象.
(1)、请说出点C的纵坐标的实际意义；(2)、经过多长时间，甲、乙两个容器中的水的深度相等？(3)、如果甲容器的底面积为10cm2 ， 求乙容器的底面积.
