江苏省泰州市靖江市2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 自新冠肺炎疫情发生以来，全国人民共同抗疫，靖江市积极普及科学防控知识，下面是科学防控知识的图片，图片上有图案和文字说明，其中的图案是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 在 $0$ ， $π$ ， $\frac{\sqrt{3}}{2}$ ， $\frac{22}{9}$ ，0.1010010001， $- \sqrt[3]{64}$ 这6个数中，无理数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 用直尺和圆规画一个角等于已知角，是运用了“全等三角形的对应角相等”这一性质，其全等的依据是（）

A、SAS B、ASA C、AAS D、SSS

查看试题解析
4. 在平面直角坐标系中，若P $(- 1, 3)$ 与Q关于 $y$ 轴对称，则Q的坐标为（）

A、 $(1, 3)$ B、 $(- 1, - 3)$ C、 $(1, - 3)$ D、 $(3, - 1)$

查看试题解析
5. 将一次函数 $y = 2 x + 3$ 的图象向下平移4个单位得到的函数表达式为（）

A、 $y = 2 x + 7$ B、 $y = 2 x - 1$ C、 $y = - 2 x - 1$ D、 $y = 2 x + 11$

查看试题解析
6. 如图，在Rt△ABC中，∠ACB＝90°，AB＝10，AC＝8，AB的垂直平分线DE交BC的延长线于点E，则DE的长为（）

A、 $\frac{10}{3}$ B、 $\frac{25}{6}$ C、 $\frac{20}{3}$ D、 $\frac{15}{4}$

查看试题解析

二、填空题

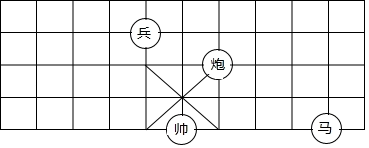
7. 用四舍五入法对数字157800精确到千位的结果是.

查看试题解析
8. 已知一次函数 $y = (k + 1) x - b$ ，若y随x的增大而减小，则k的取值范围是.

查看试题解析
9. 已知等腰三角形的两边长分别为5cm、10cm，则该等腰三角形的周长为cm.

查看试题解析
10. 中国象棋是中华民族的文化瑰宝，因趣味性强，深受大众喜爱.如图，若在象棋棋盘上建立平面直角坐标系，使“帅”位于点 $(0 ， ﹣ 2)$ ，“马”位于点 $(4 ， ﹣ 2)$ ，则“兵”位于点.

查看试题解析
11.
如图，△ABC中，D是BC上一点，AC=AD=DB，∠BAC=102°，则∠ADC=度．

查看试题解析
12. 已知一次函数 $y = x + 3$ 的图象经过点 $P (a, b)$ 和 $Q (c, d)$ ，那么 $b (c - d) - a (c - d)$ 的值为.

查看试题解析
13. 如图，一次函数y=﹣x﹣2与y=2x+m的图象相交于点P（n，﹣4），则关于x的不等式组 ${\begin{matrix} 2 x + m < - x - 2 \\ - x - 2 < 0 \end{matrix}$ 的解集为．

查看试题解析
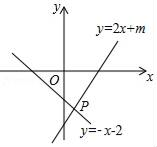14. 如图，已知∠AOB=30°，点P在射线OA上，OP=16，点E、点F在射线OB上，PE=PF，EF=6.若点D是射线OB上一动点，当∠PDE=45°时，DF的长为.

查看试题解析
15. 如图，在平面直角坐标系中，点A、点B分别在 $x$ 轴和 $y$ 轴的正半轴上运动，且AB=4，若AC=BC=5，△ABC的形状始终保持不变，则在运动的过程中，点C到原点O的最小距离为.

查看试题解析

三、解答题

16. 计算：

(1)、 $\sqrt{{(- 3)}^{2}} - (- 2) - | \sqrt{3} - 2 |$

(2)、 $\sqrt[3]{27} - {(\frac{1}{2})}^{- 2} + {(π - 2)}^{0}$

查看试题解析
17. 求下列各式中x的值.

(1)、 ${(- 2 x)}^{2} - 3 = 6$

(2)、 $3 {(x - 1)}^{3} = - 24$

查看试题解析
18. 在边长为1个单位长度的小正方形网格中，给出了△ABC（顶点是网格线的交点）.

（ 1 ）△ABC的面积为 ▲ ；

（ 2 ）在直线l上找一点P，使点P到边AB、BC的距离相等；

（ 3 ）画出△ABC关于直线l对称的图形△A₁B₁C₁；再将△A₁B₁C₁向下平移4个单位，画出平移后得到的△A₂B₂C₂.

查看试题解析
19. 如图，已知AC，BD相交于点O，AD=BC，AE⊥BD于点E，CF⊥BD于点F，BE=DF.

(1)、求证：△ADE≌△CBF

(2)、试猜想OA与OC的大小关系，并说明理由.

查看试题解析
20. 在平面直角坐标系 $x O y$ 中，点 $P (5 - m, 4 m + 5)$ .

(1)、若点P与x轴的距离为8，求m的值；

(2)、若点P在过点 $A (- 5, 3)$ 且与y轴平行的直线上，求△AOP的面积.

查看试题解析
21. 如图，某公园有两个小喷泉A、B，两个小喷泉之间的距离为25m.现要为喷泉铺设供水管道AM、BM，供水点M在小路AC上，供水点M到AB的距离MN的长为12m，BM的长为15m.

(1)、求供水点M到喷泉A、B需要铺设的管道总长；

(2)、试判断BM是否是喷泉B到小路AC的最短距离，若是，请说明理由；若不是，请求出最短距离.

查看试题解析
22. 如图，直线 $l_{1}$ ： $y = \frac{1}{2} x + 1$ 与x轴交于点D，直线 $l_{2}$ 与x轴交于点A，且过点B $(- 1 ， 5)$ ，两直线交于点C $(n ， 2)$ .

(1)、求直线 $l_{2}$ 的解析式；

(2)、在y轴上是否存在一点E，使EB+ED最小？若存在，求出点E的坐标；若不存在，请说明理由.

查看试题解析
23. 如图，△ABC是边长为12cm的等边三角形，动点M、N同时从A、B两点出发，分别沿AB、BC方向匀速移动.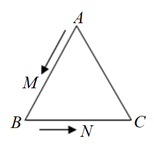

(1)、若点M的运动速度是2cm/s，点N的运动速度是4cm/s，当N到达点C时，M、N两点都停止运动，设运动时间为t（s），当t=2时，判断△BMN的形状，并说明理由；

(2)、当它们的速度都是2cm/s，当点M到达点B时，M、N两点停止运动，设点M的运动时间为t（s），则当t为何值时，△MBN是直角三角形？

查看试题解析
24. 甲、乙两辆汽车沿同一路线赶赴距出发地240千米的目的地，乙车比甲车晚出发1小时（从甲车出发时开始计时）.图中折线OABC、线段DE分别表示甲、乙两车所行路程y（千米）与时间x（小时）之间的函数关系对应的图象（线段AB表示甲出发不足1小时因故停车检修）.请根据图象所提供的信息，解决如下问题：

(1)、求乙车所行路程y与时间x的函数关系式；

(2)、求两车在途中第二次相遇时，他们距目的地还有多远？

(3)、乙车出发多长时间，甲、乙两车在途中第一次相遇？（写出解题过程）

查看试题解析
25. 如图1，点A是射线OE： $y = - x$ （x≥0）上的一点，已知 $O A^{2} = 32$ ，过点A作x轴的垂线，垂足为B，过点B作OE的平行线交∠AOB的平分线于点C.

(1)、求点A的坐标；

(2)、如图2，过点C作CG⊥AB于点G，CH⊥OE于点H，求证：CG＝CH.

(3)、①若射线OC与AB交于点D，在射线BC上是否存在一点P使得△ACP与△BDC全等，若存在，请求出点P的坐标；若不存在，请说明理由.
②在①的条件下，在平面内另有三点 $P_{1} (\sqrt{8} ， - \sqrt{8})$ 、 $P_{2}$ （4， $- \sqrt{32}$ ）、 $P_{3} (\sqrt{8} + 4 ， \sqrt{8} - 4)$ ，请你判断也满足△ACP与△BDC全等的点是 .（写出你认为正确的点）

查看试题解析