江苏省连云港市海州区2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数中，其中为无理数的是（）

A、3.14 B、 $\sqrt{5}$ C、 $\sqrt{9}$ D、 $- 5$

查看试题解析
2. 在平面直角坐标系中，点P（－3，5）关于x轴的对称点的坐标是（）

A、（3，－5） B、（－3，－5） C、（3，5） D、（5，－3）

查看试题解析
3. 由下列条件不能判定 $Δ A B C$ 为直角三角形的是（）

A、 $∠ A + ∠ B = ∠ C$ B、 $a ： b ： c = 1 ： 1 ： 2$ C、 $(b + c) (b - c) = a^{2}$ D、 $a = 1$ ， $b = \sqrt{2}$ ， $c = \sqrt{3}$

查看试题解析
4. 一次函数y=2x+1的图象不经过（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 用四舍五入法，865600精确到千位的近似值是（）

A、 $8.65 \times 10^{5}$ B、 $8.66 \times 10^{5}$ C、 $8.656 \times 10^{5}$ D、865000

查看试题解析
6. 在△ABC中和△DEF中，已知BC=EF，∠C=∠F，增加下列条件后还不能判定△ABC≌△DEF的是（　　）

A、AC=DF B、∠B=∠E C、∠A=∠D D、AB=DE

查看试题解析
7. 如图已知 $Δ A B C$ 中， $A B = A C = 12 c m$ ， $∠ B = ∠ C$ ， $B C = 8 c m$ ，点D为 $A B$ 的中点.如果点P在线段 $B C$ 上以 $2 c m / s$ 的速度由B点向C点运动，同时，点Q在线段 $C A$ 上由C点向A点运动.若点Q的运动速度为v，则当 $Δ B P D$ 与 $Δ C Q P$ 全等时，v的值为（）

A、1 B、3 C、1或3 D、2或3

查看试题解析
8. 如图， $∠ M O N = 90 °$ ，已知 $Δ A B C$ 中， $A C = B C = 10$ ， $A B = 12$ ， $Δ A B C$ 的顶点A、B分别在边 $O M$ 、 $O N$ 上，当点B在边 $O N$ 上运动时，点A随之在边 $O M$ 上运动， $Δ A B C$ 的形状保持不变，在运动过程中，点C到点O的最大距离为（）

A、12.5 B、13 C、14 D、15

查看试题解析

二、填空题

9. 25的平方根是 .

查看试题解析
10. 若点 $(6, n)$ 在函数 $y = - \frac{1}{3} x$ 的图象上，则 $n =$ .

查看试题解析
11. 若无理数a满足1<a<4，请你写出一个符合条件的无理数。

查看试题解析
12. 在一次函数y=（k﹣3）x+2中，y随x的增大而减小，则k的取值.

查看试题解析
13. 如图，等腰 $Δ A B C$ 中， $A B = A C$ ， $B C = 10$ ， $B D ⊥ A C$ 于D，且 $B D = 8$ .则 $S_{Δ A B C} =$ .

查看试题解析
14. 如图，在 $R t Δ A B C$ 中， $∠ A = 90 °$ ， $∠ A B C$ 的平分线 $B D$ 交 $A C$ 于点D， $D E$ 是 $B C$ 的垂直平分线，点E是垂足.若 $D C = 2$ ， $A D = 1$ ，则 $B E$ 的长为.

查看试题解析
15. 如图所示的折线 $A B C$ 为某地向香港地区打电话需付的通话费y（元）与通话时间 $t (m i n)$ 之间的函数关系，则通话 $8 m i n$ 应付通话费元.

查看试题解析
16. 矩形 $O A B C$ 在平面直角坐标系中的位置如图所示，点B的坐标为 $(6 ， 8)$ ，点D是 $O A$ 的中点，点E在线段 $A B$ 上，当 $Δ C D E$ 的周长最小时，点E的坐标是.

查看试题解析

三、解答题

17. 计算与求解

(1)、计算： $\sqrt{16} + \sqrt[3]{- 27} - {(- \frac{1}{2})}^{0}$

(2)、求式中x的值： ${(2 x - 1)}^{2} = 36$

查看试题解析
18. 已知：如图， $A B / / C D$ ， $D F ⊥ B C$ ， $A E ⊥ B C$ ， $C E = B F$ .求证： $D F = A E$ .

查看试题解析
19. 如图，在平面直角坐标系中， $A (1 ， 2) ， B (3 ， 1) ， C (- 2 ， - 1)$ .

(1)、在图中作出 $Δ A B C$ 关于y轴对称的 $Δ A_{1} B_{1} C_{1}$ ；

(2)、 $Δ A_{1} B_{1} C_{1}$ 的面积为.

查看试题解析
20. 已知直线 $y = k x + b$ 经过点 $A (5 ， 0)$ ， $B (1 ， 4)$ .

(1)、求直线 $A B$ 的解析式；

(2)、若直线 $y = 2 x - 4$ 与直线 $A B$ 相交于点C，求点C的坐标；

(3)、根据图象，写出关于x的不等式 $2 x - 4 < k x + b$ 的解集.

查看试题解析
21. 如图，四边形OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处.

(1)、求点E的坐标；

(2)、求点D的坐标.

查看试题解析
22. 剧院举行新年专场音乐会，成人票每张20元，学生票每张5元，剧院制定了两种优惠方案，方案1：购买一张成人票赠送一张学生票；方案2：按总价的 $90 %$ 付款.某校有4名老师与若干名（不少于4人）学生听音乐会.

(1)、设学生人数为x（人），付款总金额为y（元），分别表示这两种方案；

(2)、请计算并确定出最节省费用的购票方案.

查看试题解析
23. 如图，在 $Δ A B C$ 中， $∠ B A C = 90 °$ ， $A B = 6 c m$ ， $B C = 10 c m$ ，点D在线段 $A C$ 上，且 $C D = 2 c m$ ，动点P从距A点 $10 c m$ 的E点出发，以每秒 $2 c m$ 的速度沿射线 $E A$ 的方向运动了t秒.

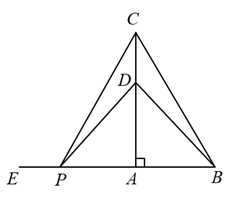(1)、 $A D$ 的长为；

(2)、写出用含有t的代数式表示 $A P$ ，并写出自变量的取值范围；

(3)、直接写出多少秒时， $Δ P B C$ 为等腰三角形.

查看试题解析
24. 如图1， $O A = 2$ ， $O B = 4$ ，以A点为顶点、 $A B$ 为腰在第三象限作等腰直角 $Δ A B C$ .

(1)、求点C的坐标；

(2)、如图2，P是y轴负半轴上一个动点，当P点向y轴负半轴向下运动时，若以P为直角顶点， $P A$ 为腰作等腰直角 $Δ A P D$ ，过点D作 $D E ⊥ x$ 轴于点E，求 $O P - D E$ 的值；

(3)、如图3，已知点F坐标为 $(- 3 ， - 3)$ ，当G在y轴运动时，作等腰直角 $Δ F G H$ ，并始终保持 $∠ G F H = 90 °$ ， $F G$ 与y轴交于点 $G (0 ， m)$ ， $F H$ 与x轴交于点 $H (n ， 0)$ ，求m、n满足的数量关系.

查看试题解析
25. 甲乙两人匀速从同一地点到1500米处的图书馆看书，甲出发5分钟后，乙以50米/分的速度沿同一路线行走.设甲乙两人相距s（米），甲行走的时间为t（分），s关于t的函数函数图象的一部分如图所示.

(1)、求甲行走的速度；

(2)、在坐标系中，补画s关于t函数图象的其余部分；

(3)、问甲、乙两人何时相距360米？

查看试题解析
26.

(1)、问题：如图①，在 $R t Δ A B C$ 中， $A B = A C$ ，D为 $B C$ 边上一点（不与点 $B ， C$ 重合），将线段 $A D$ 绕点A逆时针旋转 $90 °$ 得到 $A E$ ，连接 $E C$ ，则线段 $B C$ ， $D C$ ， $E C$ 之间满足的等量关系式为；

(2)、探索：如图②，在 $R t Δ A B C$ 与 $R t Δ A D E$ 中， $A B = A C$ ， $A D = A E$ ，将 $Δ A D E$ 绕点A旋转，使点D落在 $B C$ 边上，试探索线段 $A D$ ， $B D$ ， $C D$ 之间满足的等量关系，并证明结论；

(3)、应用：如图3，在四边形 $A B C D$ 中， $∠ A B C = ∠ A C B = ∠ A D C = 45 °$ .若 $B D = 12$ ， $C D = 4$ ，求 $A D$ 的长.

查看试题解析