湖南省长沙市天心区明德教育集团2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在代数式 $\frac{\sqrt{x - 1}}{3}$ 中，字母x的取值范围是（　　）

A、x＞1 B、x≥1 C、x＜1 D、x $\leq \frac{1}{3}$

查看试题解析
3. 下列运算中，结果正确的是（　　）

A、 ${(a + b)}^{2} = a^{2} + b^{2}$ B、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ C、 $(a - 1) (a + 1) = a^{2} - 1$ D、 $a^{6} \div a^{2} = a^{3}$

查看试题解析
4. 已知三角形两边长分别为4和8，则该三角形第三边的长可能是（　　）

A、4 B、5 C、12 D、13

查看试题解析
5. 已知一个多边形的内角和为1080°，则这个多边形是（）

A、九边形 B、八边形 C、七边形 D、六边形

查看试题解析
6. 若分式 $\frac{x - 2}{x + 1}$ 的值为0，则x的值为（）

A、﹣1 B、0 C、2 D、﹣1或2

查看试题解析
7. 使两个直角三角形全等的条件是（）

A、一个锐角对应相等 B、两个锐角对应相等 C、一条边对应相等 D、斜边及一条直角边对应相等

查看试题解析
8. 如图，已知AB＝AC，AD是△ABC的高，下列结论不一定正确的是（　　）

A、∠B＝60° B、∠B＝∠C C、∠BAD＝∠CAD D、BD＝CD

查看试题解析
9. 如果代数式x²+mx+36是一个完全平方式，那么m的值为（）

A、6 B、﹣12 C、±12 D、±6

查看试题解析
10. 如图，△ABC中，边AB的垂直平分线与AC交于点D，与AB交于点E，已知AC＝6，BC＝4，则 $△ B C D$ 的周长是（　　）

A、7 B、8 C、9 D、10

查看试题解析
11. 如图，已知∠ABC＝∠DEF，AB＝DE，添加以下条件，不能判定△ABC≌△DEF的是（　　）

A、∠A＝∠D B、∠ACB＝∠DFE C、AC＝DF D、BE＝CF

查看试题解析
12. 已知x＝ $\sqrt{5}$ +2，则代数式x²﹣x﹣2的值为（　　）

A、9+5 $\sqrt{5}$ B、9+3 $\sqrt{5}$ C、5+5 $\sqrt{5}$ D、5+3 $\sqrt{5}$

查看试题解析

二、填空题

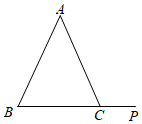
13. 分解因式：a²－4＝.

查看试题解析
14. 化简： $\frac{x^{2}}{x + 1} + \frac{x}{x + 1}$ ＝.

查看试题解析
15. 如图，已知∠ACP＝115°，∠B＝65°，则∠A＝.

查看试题解析
16. 如图，Rt△ABC中，∠C＝90°，∠A＝30°，AB＝8cm，则BC＝cm.

查看试题解析
17. 如图，在△ABC中，∠C＝90°，以A为圆心，任意长为半径画弧，分别交AC，AB于点M，N，再分别以M，N为圆心，大于 $\frac{1}{2}$ MN长为半径画弧，两弧交于点O，作射线AO，交BC于点E.已知CB＝8，BE＝5，则点E到AB的距离为.

查看试题解析
18. 如图，∠A＝∠B＝90°，AB＝100，E，F分别为线段AB和射线BD上的一点，若点E从点B出发向点A运动，同时点F从点B出发向点D运动，二者速度之比为2：3，运动到某时刻同时停止，在射线AC上取一点G，使△AEG与△BEF全等，则AG的长为.

查看试题解析

三、解答题

19. 计算： $\sqrt{6} \div \sqrt{3}$ +（ $\frac{1}{4}$ ）^﹣1﹣|1- $\sqrt{2}$ |+（1901﹣ $\sqrt{2021}$ ）⁰.

查看试题解析
20. 先化简，再求值：（x+y）（x﹣y）﹣x（x+2y）+3xy，其中x＝1，y＝3.

查看试题解析
21. 如图，已知△ABC的三个顶点在格点上，网格上最小的正方形的边长为1.

(1)、点A关于x轴的对称点坐标为，点B关于y轴的对称点坐标为.

(2)、作出与△ABC关于x轴对称的图形△A₁B₁C₁.

(3)、求△ABC的面积.

查看试题解析
22. 解分式方程：

(1)、 $\frac{3}{2 x} = \frac{2}{x + 1}$ ；

(2)、 $\frac{1}{x + 1} + \frac{2}{x - 1} = \frac{4}{x^{2} - 1}$ .

查看试题解析
23. 如图，已知点D、E是△ABC内两点，且∠BAE＝∠CAD，AB＝AC，AD＝AE.

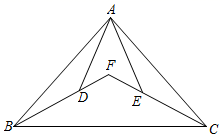(1)、求证： $△ A B D ≌ △ A C E$ .

(2)、延长BD、CE交于点F，若 $∠ B A C = 86 °$ ， $∠ A B D = 20 °$ ，求 $∠ B F C$ 的度数.

查看试题解析
24. 明德中学需要购进甲、乙两种笔记本电脑，经调查，每台甲种电脑的价格比每台乙种电脑的价格少0.2万元，且用12万元购买的甲种电脑的数量与用20万元购买的乙种电脑的数量相同.

(1)、求每台甲种电脑、每台乙种电脑的价格分别为多少万元；

(2)、学校计划用不超过34万元购进甲、乙两种电脑共80台，其中乙种电脑的数量不少于甲种电脑数量的1.5倍，学校有哪几种购买方案？

查看试题解析
25. 在平面直角坐标系中，已知A（x，y），且满足x²+6x+y²﹣6y+18＝0，过点A作AB⊥y轴，垂足为B.

(1)、求A点坐标；

(2)、如图1，若分别以AB、AO为边作等边△ABC和等边△AOD，试判定线段AC和CD的数量关系和位置关系，并说明理由；

(3)、如图2，若在x轴正半轴上取一点M，连接BM并延长至N，以BN为直角边作等腰Rt△BNE，∠BNE＝90°，过点A作AF∥y轴交BE于点F，连接MF，设OM＝a，MF＝b，AF＝c，试证明： $\frac{1}{a} + \frac{1}{b} = \frac{c}{a b}$ .

查看试题解析
26. 对于平面直角坐标系xOy中的线段AB和点M，给出定义：若M满足：MA＝MB，则称M是线段AB的“富强点”，其中，当0°＜∠AMB＜60°，称M为线段AB的“民主点”；当60°≤∠AMB≤180°时，则称M为“文明点”.

(1)、如图1，点A，B的坐标分别为（0，2），（2，0），则在坐标M₁（0，0），M₂（2，3），M₃（4，4）中，是线段AB的“富强点”为：；是线段AB的“文明点”为.

(2)、如图2，点A的坐标为（﹣3，0），AB＝2 $\sqrt{3}$ ，且∠OAB＝30°.若M为线段AB的“民主点”，直接写出M的横坐标m的取值范围；

(3)、在（2）的条件下，点P为y轴上的动点（不与B重合且BP≠AB），若T为AB的“富强点”，当线段TB和TP的和最小时，求T′的坐标，以及此时T′关于直线AB的对称点S的坐标.

查看试题解析