湖南省娄底市涟源市2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 的平方根是( )A、3 B、 C、9 D、2. 下列说法中,正确的个数为( )
①无限小数都是无理数:
②无限不循环小数都是无理数;
③无理数都是无限小数:
④无理数也有负数;
⑤无理数分为正无理数、零、负无理数.
A、1个 B、2个 C、3个 D、4个3. 若分式 有意义,则a的取值范围是( )A、a=0 B、a="1" C、a≠﹣1 D、a≠04. 2a与3a的大小关系( )A、2a<3a B、2a>3a C、2a=3a D、不能确定5. 下列运算正确的是( )A、 - = B、 =2 C、 - = D、 =2-6. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、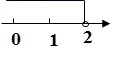 C、
C、 D、
D、 7. 下列运算结果正确的是( )A、 =﹣3 B、(﹣ )2=2 C、 ÷ =2 D、 =±48. 下列各式是分式的是( )A、 B、 C、 D、9. 若等腰三角形的两条边长分别为2和4,则该等腰三角形的周长为( )A、6 B、8 C、10 D、8或1010. 分式方程 的解为( )A、x=1 B、x=2 C、x=3 D、x=411. 如图,在折纸活动中,小明制作了一张 纸片,点 分别是边 上的点,将 沿着 折叠压平,A与 重合,若 ,则 ( )
7. 下列运算结果正确的是( )A、 =﹣3 B、(﹣ )2=2 C、 ÷ =2 D、 =±48. 下列各式是分式的是( )A、 B、 C、 D、9. 若等腰三角形的两条边长分别为2和4,则该等腰三角形的周长为( )A、6 B、8 C、10 D、8或1010. 分式方程 的解为( )A、x=1 B、x=2 C、x=3 D、x=411. 如图,在折纸活动中,小明制作了一张 纸片,点 分别是边 上的点,将 沿着 折叠压平,A与 重合,若 ,则 ( ) A、 B、 C、 D、12. 如图,在 中, , , 是 的中线,且 , 是 的角平分线, 交 的延长线于点F,则 的长为( )
A、 B、 C、 D、12. 如图,在 中, , , 是 的中线,且 , 是 的角平分线, 交 的延长线于点F,则 的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 某红外线波长为 ,用科学记数法表示这个数是 .14. “两直线平行,内错角相等”的逆命题是 .15. 若分式 的值为0,则x的值为 .16. 化简 的结果是 .
17. 不等式 的解集是 ,则a的取值范围是.18. 已知三角形的三边分别为a,b,c , 其中a , b满足 ,那么这个三角形的第三边c的取值范围是.三、解答题
-
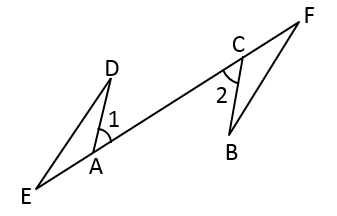
19. 计算: .20. 解不等式组:21. 如图,已知 , , ,点E,F在直线 上.
求证: .
 22. 先化简,再求值: ,其中实不等x式 的非正整数解.23. 已知:如图,在△ABC中,∠A=30°,∠B=60°,E为AB的中点.
22. 先化简,再求值: ,其中实不等x式 的非正整数解.23. 已知:如图,在△ABC中,∠A=30°,∠B=60°,E为AB的中点. (1)、作∠B的平分线BD,交AC于点D;(要求:尺规作图,保留作图痕迹,不必写作法和证明);(2)、连接DE,求证:△ADE≌△BDE.24.(1)、从计算过程中找出规律,可知 ;用含有n(n是正整)的等式表示上述变化规律;(2)、利用上述变化规律计算:
(1)、作∠B的平分线BD,交AC于点D;(要求:尺规作图,保留作图痕迹,不必写作法和证明);(2)、连接DE,求证:△ADE≌△BDE.24.(1)、从计算过程中找出规律,可知 ;用含有n(n是正整)的等式表示上述变化规律;(2)、利用上述变化规律计算:的值.
