湖南省怀化市中方县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 分式 有意义,则x、y满足的条件是( )A、 B、 C、 D、2. 下列各数中,最大的是( )A、 B、 C、 D、3. 下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )A、3cm,4cm,8cm B、8cm,7cm,15cm C、13cm,12cm,20cm D、5cm,5cm,11cm4. 新冠病毒呈颗粒圆形或椭圆形,体积很小,直径大概在60-140纳米之间(1纳米=0.000000001米),特别不容易防护.假若一颗新冠病毒的直径是75纳米,用科学记数法表示这颗病毒的直径,正确的是( )A、 米 B、 米 C、 米 D、 米5. 下列命题是假命题的是( )A、若x是无理数,则x是实数 B、若 ,则 C、若 ,则 D、两个内角相等的三角形是等腰三角形6. 下列计算正确的是( )A、 B、 C、 D、7. 如图,在△ABC中,点D在BC上,AB=AD=DC,∠B=70°,则∠C的度数为( )
 A、30° B、35° C、40° D、45°8. 如图,若 ,则 的度数是( )
A、30° B、35° C、40° D、45°8. 如图,若 ,则 的度数是( )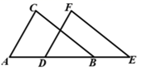 A、 B、 C、 D、9. 不等式 的解集是( )A、 B、 C、 D、10. 等腰三角形的一个外角是100° ,它的顶角的是( )A、80° B、20° C、20°或80° D、100°
A、 B、 C、 D、9. 不等式 的解集是( )A、 B、 C、 D、10. 等腰三角形的一个外角是100° ,它的顶角的是( )A、80° B、20° C、20°或80° D、100°二、填空题
-
11. 计算: .12. 某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分,娜娜的得分要超过90分,设她答对了x道题,则根据题意,可列不等式为.13. 如图,∠BAC=∠ABD,请你添加一个条件: , 能使△ABD≌△BAC(只添一个即可).
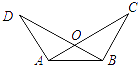 14. 如图,在 中,D , E分别是BC , AD的中点, ,则 的值是 .
14. 如图,在 中,D , E分别是BC , AD的中点, ,则 的值是 . 15. 上午10时,一艘船从A处出发以每小时25海里的速度向正北航行,中午12时到达B处,从A、B两点观望灯塔C,测得 , ,则B到灯塔C的距离是海里.
15. 上午10时,一艘船从A处出发以每小时25海里的速度向正北航行,中午12时到达B处,从A、B两点观望灯塔C,测得 , ,则B到灯塔C的距离是海里.
三、解答题
-
16. 计算:(1)、(2)、17. 解答下列两题:(1)、计算:(2)、若不等式组 的解集是 ,求a的取值范围.18. 在解答“先化简式子 ,再选一个你认为合适的整数x代入求值”这个题时,小明选取 ,计算得原式的值为 .(1)、你认为小明的计算正确吗?为什么?(2)、请你写出你的解答过程.19. 已知不等式组 .(1)、解这个不等式组,并把它的解集在数轴上表示出来.(2)、若a是这个不等式组的最小整数解,求 的值.20. 如图,在△ABC中,∠ACB=70 °,∠B=65°,AD⊥BC,CE⊥AB,垂足分别为D,E.
 (1)、求证:AE=CE.(2)、求证:△AEF≌△CEB.21. 如图.在△ABC中,∠C=90 °,∠A=30°.
(1)、求证:AE=CE.(2)、求证:△AEF≌△CEB.21. 如图.在△ABC中,∠C=90 °,∠A=30°. (1)、用直尺和圆规作AB的垂直平分线,分别交AB、AC于D、E,交BC的延长线于F,连接EB.(不写作法,保留作图痕迹)(2)、求证:EB平分∠ABC.(3)、求证:AE=EF.22. 倡导健康生活推进全民健身,某社区去年购进A,B两种健身器材若干件,经了解,B种健身器材的单价是A种健身器材的1.5倍,用7200元购买A种健身器材比用5400元购买B种健身器材多10件.(1)、A,B两种健身器材的单价分别是多少元?(2)、若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共50件,且费用不超过21000元,请问:A种健身器材至少要购买多少件?23. 如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
(1)、用直尺和圆规作AB的垂直平分线,分别交AB、AC于D、E,交BC的延长线于F,连接EB.(不写作法,保留作图痕迹)(2)、求证:EB平分∠ABC.(3)、求证:AE=EF.22. 倡导健康生活推进全民健身,某社区去年购进A,B两种健身器材若干件,经了解,B种健身器材的单价是A种健身器材的1.5倍,用7200元购买A种健身器材比用5400元购买B种健身器材多10件.(1)、A,B两种健身器材的单价分别是多少元?(2)、若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共50件,且费用不超过21000元,请问:A种健身器材至少要购买多少件?23. 如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动. (1)、若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;(2)、若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(3)、若Q以(2)中的速度从C点出发,同时P以原来的速度从B点出发,在△ABC的三边上逆时针运动,问:经过多少时间P、Q两点第一次相遇?在何处相遇?
(1)、若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;(2)、若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(3)、若Q以(2)中的速度从C点出发,同时P以原来的速度从B点出发,在△ABC的三边上逆时针运动,问:经过多少时间P、Q两点第一次相遇?在何处相遇?