河南省郑州市登封市2020-2021学年八年级上学期数学期末考试试卷

试卷更新日期：2021-04-19 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，在4×4的正方形网格中，所有线段的端点都在格点处，则这些线段的长度是无理数的有（　　）

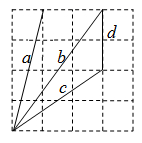A、1 条 B、2条 C、3条 D、4条

查看试题解析
2. 下列计算正确的是（　　）

A、 $\sqrt{8} - \sqrt{2} = \sqrt{2}$ B、 $\sqrt{{(- 2)}^{2}} = - 2$ C、 $\sqrt{6} \div \sqrt{3} = \sqrt{3}$ D、 $\sqrt{2} \times \sqrt{3} = \sqrt{5}$

查看试题解析
3. 随着“双十二”的临近，各平台进行各种抽奖活动.某数学兴趣小组将如图所示的红包放入坐标系中，现将红包上点A的横坐标不变、纵坐标乘以-1，则得到的新点与点A的位置关系是（　　）

A、关于x轴对称 B、关于y 轴对称 C、关于原点对称 D、没有对称关系

查看试题解析
4. 随着冬季的来临，流感进入高发期.某校为有效预防流感，购买了A，B，C，D四种艾条进行消毒，它们的单价分别是30元，25元，20元，18元.四种艾条的购买比例如图所示，那么所购买艾条的平均单价是（　　）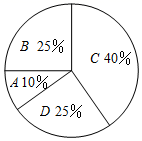

A、22.5元 B、23.25元 C、21.75元 D、24元

查看试题解析
5. 如图，在数轴上作长、宽分别为2和1的长方形，以原点为圆心，长方形对角线的长为半径画弧，与数轴相交于点A.若点A对应的数字为a，则下列说法正确的是（　　）

A、a>-2.3 B、a<-2.3 C、a=-2.3 D、无法判断

查看试题解析
6. 毕达哥拉斯树，也叫“勾股树”，是由毕达哥拉斯根据勾股定理所画出来的一个可以无限重复的树形图形，其中所有的四边形都是正方形，所有的三角形都是直角三角形.若正方形A，B，C，D的边长分别是2，3，1，2，则△正方形E的边长是（　　）

A、18 B、8 C、2 $\sqrt{2}$ D、3 $\sqrt{2}$

查看试题解析
7. 某学校操场是周长为400 m 的长方形，且长比宽的2倍少40m.若设该长方形的长为 x，宽为y，则可列方程组为（　　）

A、 ${\begin{array}{l} x + y = 400 \\ 2 y - 40 = x \end{array}$ B、 ${\begin{array}{l} x + y = 400 \\ 2 y + 40 = x \end{array}$ C、 ${\begin{array}{l} x + y = 200 \\ 2 y - 40 = x \end{array}$ D、 ${\begin{array}{l} x + y = 200 \\ 2 y + 40 = x \end{array}$

查看试题解析
8. 一次函数y=kx＋b中，x 与γ的部分对应值如下表所示，则下列说法正确的是（　　）

ｘ

…

-1

0

1

2

…

ｙ

…

5

2

-1

-4

…

A、x 的值每增加1，y的值增加 3，所以k=3 B、x=2是方程 kx＋b=0的解 C、函数图象不经过第四象限 D、当x>1时，y<-1

查看试题解析
9. 如图所示直线反映了某公司产品的销售成本和销售收入与销售量之间的关系，则下列说法错误的是（　　）

A、直线l₁反映了该公司产品的销售收入与销售量之间的关系 B、未开始销售时，该公司为销售所花的成本为2000元 C、当销售量大于 4吨时，该公司赢利 D、每销售1吨产品，销售收入为 500 元

查看试题解析
10. 学习勾股定理后，老师布置的课后作业为“利用绳子（绳子足够长）和卷尺，测量学校教学楼的高度”，某数学兴趣小组的做法如下：①将绳子上端固定在教学楼顶部，绳子自由下垂，再垂直向外拉到离教学楼底部3m远处，在绳子与地面的交点处将绳子打结；②将绳子继续往外拉，使打结处离教学楼的距离为6m，此时测得绳结离地面的高度为 1m，则学校教学楼的高度为（　　）

A、11 m B、13 m C、14 m D、15 m

查看试题解析

二、填空题

11. $\sqrt{\frac{9}{4}}$ =.

查看试题解析
12. 编写一个二元一次方程组，使它的解是 ${\begin{array}{l} x = - 2 \\ y = 3 \end{array}$ 则该方程组可以是.

查看试题解析
13. 若函数y=（m-3） $x^{| m - 2 |}$ ＋m-1是一次函数，则m的值为.

查看试题解析
14. 如图，圆柱形容器外壁距离下底面3cm的A处有一只蚂蚁，它想吃到正对面外壁距离上底面3cm的B处的米粒，若圆柱的高为12cm，底面周长为24 cm.则蚂蚁爬行的最短距离为.

查看试题解析
15. 如图，在平面直角坐标系中，长方形OABC的边OA 在x轴上，OC在y轴上，OA=1，OC=2，对角线 AC的垂直平分线交AB 于点E，交AC于点D.若y轴上有一点P（不与点C重合），能使△AEP是以为 AE 为腰的等腰三角形，则点 P的坐标为.

查看试题解析

三、解答题

16.

(1)、计算:
① $\frac{\sqrt{27} + \sqrt{12}}{\sqrt{3}}$ ；

②(2 $\sqrt{3}$ ＋3 $\sqrt{2}$ )(2 $\sqrt{3}$ -3 $\sqrt{2}$ ).

(2)、解方程:
①4(x-1)²-9 =0；

②8x³＋125=0.

查看试题解析
17. 为迎接“阳光大课间”检查活动，某校计划为学生购买一批白色运动鞋.现从全校随机抽取了部分学生进行鞋号统计，将统计结果绘制成如图所示的统计图，请你根据信息，解答下列问题：

(1)、本次调查共抽取了人，扇形统计图中m的值为；

(2)、所抽取学生鞋码的中位数是；

(3)、若该学校有1600名学生，根据统计信息，你建议学校多购买哪个号的鞋?建议购买多少双?

查看试题解析
18. 如图是某体育广场上的秋千，秋千静止时，其下端离地面0.7m，秋千荡到最高位置时，其下端离地面1.2 m，此时秋千与静止位置时的水平距离为1.5 m，请你根据以上数据计算秋千摆绳的长度.

查看试题解析
19. 随着新冠肺炎疫情的持续，某学校计划购进一批防疫物品，经过市场调查得知：某品牌洗手液和消毒水原来的单价和为50元.因政府市场调控，洗手液降价10%，消毒水降价20%，调价后，两种物品的单价和比原来降低了16%.请你用二元一次方程组的知识计算该学校购买 200 瓶洗手液和 300 瓶消毒水共需要多少钱.

查看试题解析
20. 如图，网格中每个小正方形的边长均为1，点A，B都在格点上，点A的坐标为（-1，4），点B的坐标为（-3，2），请按要求回答下列问题：

(1)、请你在网格中建立合适的平面直角坐标系；

(2)、在y轴左侧找一格点C，使△ABC 是以AB为腰的等腰直角三角形，则点C的坐标为， △ABC的周长是；

(3)、在x轴上是否存在点P，使△ABP的周长最小?若存在，请求出点P的坐标；若不存在，请说明理由.

查看试题解析
21. A，B，C三个村庄依次在一条笔直的公路旁，甲从A村庄出发沿着这条公路匀速去B村庄，乙从C村庄出发沿着这条公路匀速去A村庄，当其中一人到达目的地时，另一人也随之停止运动.甲、乙与B村庄的距离y，y₂ ，与甲的行驶时间t 之间的函数关系如图所示.请根据所给图象解答下列问题：

(1)、填空：A，B两村庄之间的距离为km，乙比甲晚出发h；乙的速度为km/h，甲的速度为km/h；

(2)、求乙从C村庄到B村庄的行驶过程中，与B村庄的距离y₂与甲行驶的时间t之间的函数关系式；

(3)、请直接写出当t为何值时，甲与乙相遇.

查看试题解析
22. “游山水、寻特色、览风情、悟心得”，为推动文旅产业全面复苏，某旅游公司推出河南省十大景点畅游活动，活动内容如下：游客免费注册普通会员，旅游门票费用打八折；游客注册 VIP 会员，需要支付 100 元的注册费用，旅游门票费用打六折.活动期间，某旅游门票原价为x元，注册普通会员所需费用为y₁元，注册， VIP 会员所需费用为y₂元.

(1)、求出y₁ ， y₂关于x的函数解析式；

(2)、若旅游门票原价为1000元，则选择哪种活动更划算?

(3)、当旅游门票原价为多少元时，选择两种活动所需费用相同?

(4)、根据图象，请直接写出如何选择活动方式更划算.

查看试题解析
23. 如图1，一次函数y= $\frac{3}{4}$ x+3的图象与x 轴相交于点A，与y 轴相交于点 B，点 D是直线 AB 上的一个动点， CD⊥x 轴于点C，点 P是射线 CD 上的一个动点.

(1)、求点A，B的坐标；

(2)、如图2，当点D在第一象限，且AB =BD时，将△ACP沿着 AP翻折，当点C的对应点C'落在直线AB上时，求点P的坐标.

(3)、点D在运动过程中，当△OCD的面积是△OAD面积的2倍时，请直接写出点D的坐标.

查看试题解析

ｘ	…	-1	0	1	2	…
ｙ	…	5	2	-1	-4	…