贵州省遵义市桐梓县2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 下列图形中不是轴对称图形的是( )A、
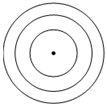 B、
B、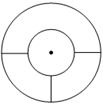 C、
C、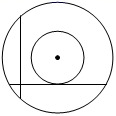 D、
D、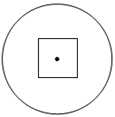 2. 下列图形中具有稳定性的是( )A、等边三角形 B、正方形 C、平行四边形 D、梯形3. 要使分式 有意义,则x的取值范围是( )A、 B、 C、 D、4. 以下列各组线段长(单位:厘米)为边能组成三角形的是( )A、 B、 C、 D、5. 根据下列条件,能判定 的是( )A、 B、 C、 D、6. 的计算结果是( )A、 B、 C、 D、7. 等腰三角形的一边长为6,另一边长为4,则其周长为( )A、 B、 C、 或 D、以上都不是8. 若 的值为1,则 的值为( )A、 B、 C、 D、9. 为了提高广大市民的禁毒意识和防毒拒毒能力,某县准备修建一个禁毒文化广场,如图是该文化广场设计图纸的一部分,其面积表示错误的是( )
2. 下列图形中具有稳定性的是( )A、等边三角形 B、正方形 C、平行四边形 D、梯形3. 要使分式 有意义,则x的取值范围是( )A、 B、 C、 D、4. 以下列各组线段长(单位:厘米)为边能组成三角形的是( )A、 B、 C、 D、5. 根据下列条件,能判定 的是( )A、 B、 C、 D、6. 的计算结果是( )A、 B、 C、 D、7. 等腰三角形的一边长为6,另一边长为4,则其周长为( )A、 B、 C、 或 D、以上都不是8. 若 的值为1,则 的值为( )A、 B、 C、 D、9. 为了提高广大市民的禁毒意识和防毒拒毒能力,某县准备修建一个禁毒文化广场,如图是该文化广场设计图纸的一部分,其面积表示错误的是( )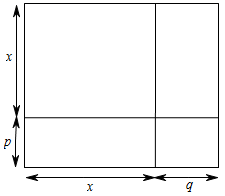 A、 B、 C、 D、10. 如图,两个全等的直角三角形重叠在一起,将其中 沿着点B到C的方向平移到 的位置, ,平移距离为 ,则 的面积为( )
A、 B、 C、 D、10. 如图,两个全等的直角三角形重叠在一起,将其中 沿着点B到C的方向平移到 的位置, ,平移距离为 ,则 的面积为( )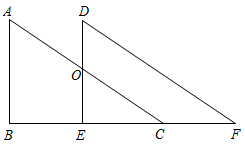 A、6 B、12 C、18 D、2411. 如图,把长方形纸片 沿对角线折叠,设重叠部分为 .下列说法错误的是( )
A、6 B、12 C、18 D、2411. 如图,把长方形纸片 沿对角线折叠,设重叠部分为 .下列说法错误的是( )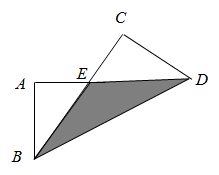 A、 B、 C、 D、△ABE≌△CDE12. 如图,在 中, , 是 边上的高, 是 边的中线, 是 的角平分线, 交 于点G,交 于点H,下面说法正确的是( )
A、 B、 C、 D、△ABE≌△CDE12. 如图,在 中, , 是 边上的高, 是 边的中线, 是 的角平分线, 交 于点G,交 于点H,下面说法正确的是( )① 的面积是 的面积的一半;② ;③ ;④ .
 A、①②③④ B、①② C、①③ D、①④
A、①②③④ B、①② C、①③ D、①④二、填空题
-
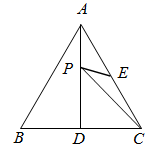
13. 某种病毒的直径为 米,用科学记数法表示为米.14. 点 关于x轴的对称点 的坐标为.15. 一个正多边形的内角和为 ,则这个多边形的外角的度数为.16. 如图, 是等边三角形, 是 边上的高,且 是 的中点,P是 上的一个动点, 与 的和最小为.
三、解答题
-
17.(1)、因式分解: ;(2)、利用因式分解计算: .18. 因式分解:(1)、(2)、19. 先化简,再求值: ,请你从 中任选一个你喜欢的数代入求值.20. 如图,平面直角坐标系中 的顶点均在格点上,点A的坐标为 .
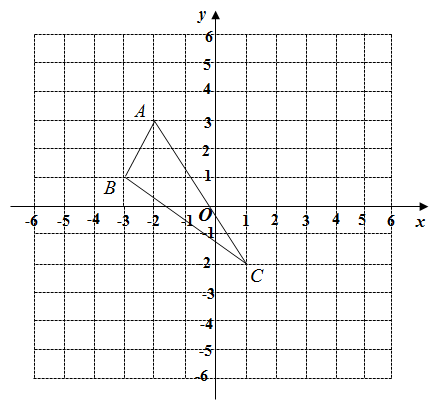
( 1 )请在图中作出与 关于y轴对称的 ;
( 2 )写出点 和点 的坐标.
( 3 )求 的面积.
21. 如图, .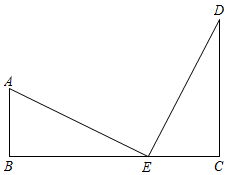 (1)、求证: ;(2)、试判断 与 的位置关系,并说明理由.22. 如图,在 中, 的垂直平分线 交 于点D,连接 ,若 .
(1)、求证: ;(2)、试判断 与 的位置关系,并说明理由.22. 如图,在 中, 的垂直平分线 交 于点D,连接 ,若 .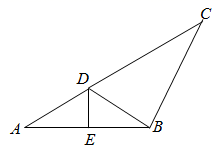 (1)、求证:(2)、求 的长.23. 为切实做好新冠肺炎的防控工作,贯彻落实“预防为主,安全第一”的方针,某学校计划购买A、B两种品牌的消毒液,已知B品牌消毒液每瓶的价格是A品牌消毒液每瓶价格的 倍少 元,用 元买A品牌消毒液的数量与用 元购买B品牌消毒液的数量相同.(1)、求A、B两种品牌消毒液每瓶的价格各是多少元?(2)、若该校一次性购买A、B两种品牌的消毒液分别为 瓶和 瓶,请问该校此次购买消毒液花费为多少元?24. 如图, 中, ,现有两点 分别从点A点B同时出发,沿三角形的边运动,已知点 的速度为每秒 个单位长度,点N的运度为每秒 个单位长度,当点M到达B点时, 同时停止运动,设运动时间为t秒.
(1)、求证:(2)、求 的长.23. 为切实做好新冠肺炎的防控工作,贯彻落实“预防为主,安全第一”的方针,某学校计划购买A、B两种品牌的消毒液,已知B品牌消毒液每瓶的价格是A品牌消毒液每瓶价格的 倍少 元,用 元买A品牌消毒液的数量与用 元购买B品牌消毒液的数量相同.(1)、求A、B两种品牌消毒液每瓶的价格各是多少元?(2)、若该校一次性购买A、B两种品牌的消毒液分别为 瓶和 瓶,请问该校此次购买消毒液花费为多少元?24. 如图, 中, ,现有两点 分别从点A点B同时出发,沿三角形的边运动,已知点 的速度为每秒 个单位长度,点N的运度为每秒 个单位长度,当点M到达B点时, 同时停止运动,设运动时间为t秒.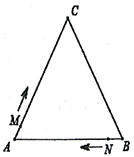 (1)、当 时, , ;(用含t的代数式表示)(2)、当点 在边 上运动时,是否存在某个时刻,使得 成立,若成立,请求出此时点M运动的时间;若不成立请说明理由.(3)、当点 在同一直线上运动时,求运动时间t的取值范围.
(1)、当 时, , ;(用含t的代数式表示)(2)、当点 在边 上运动时,是否存在某个时刻,使得 成立,若成立,请求出此时点M运动的时间;若不成立请说明理由.(3)、当点 在同一直线上运动时,求运动时间t的取值范围.