广西壮族自治区贵港市覃塘区2020-2021学年八年级上学期数学期末考试试卷
试卷更新日期:2021-04-19 类型:期末考试
一、单选题
-
1. 8的立方根是( )A、 4 B、 C、2 D、2. 将“x的2倍与5的和不是正数”用不等式表示为( )A、 B、 C、 D、3. 若 ,则m与3的关系一定是( )A、 B、 C、 D、4. 估算 的值在( )A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间5. 已知等腰三角形的一个内角度数为 则它的底角的度数为( )A、 B、 C、 或 D、 或6. 化简 的结果是( )A、 B、 C、 D、7. 不等式组 的解集在数轴上表示正确的是( )A、
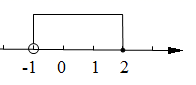 B、
B、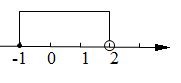 C、
C、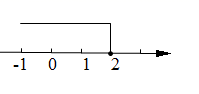 D、
D、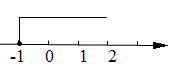 8. 下列命题中,为真命题的是( )A、 是13的算术平方根 B、三角形的一个外角大于任何一个内角 C、 是最简二次根式 D、两条直线被第三条直线所截,内错角相等9. 已知关于x的分式方程 的解是非负数,则m的取值范围是( )A、 B、 且 C、 D、 且10. 如图,点C,D分别在线段 , 上, 与 相交于点E,若 , ,则图中全等三角形的对数为( )
8. 下列命题中,为真命题的是( )A、 是13的算术平方根 B、三角形的一个外角大于任何一个内角 C、 是最简二次根式 D、两条直线被第三条直线所截,内错角相等9. 已知关于x的分式方程 的解是非负数,则m的取值范围是( )A、 B、 且 C、 D、 且10. 如图,点C,D分别在线段 , 上, 与 相交于点E,若 , ,则图中全等三角形的对数为( ) A、5对 B、4对 C、3对 D、2对11. 如图,在 中, 平分 , 平分 , 经过点O且 ,若 , , ,则 的周长是( )
A、5对 B、4对 C、3对 D、2对11. 如图,在 中, 平分 , 平分 , 经过点O且 ,若 , , ,则 的周长是( ) A、15 B、16 C、17 D、2412. 如图,在 中, , 分别是 , 边的垂直平分线,且分别与 交于点M,N连接 , .有下列四个结论:① ;② ;③ 与 是互为补角;④ 的周长与 边长相等其中正确结论的个数是( )
A、15 B、16 C、17 D、2412. 如图,在 中, , 分别是 , 边的垂直平分线,且分别与 交于点M,N连接 , .有下列四个结论:① ;② ;③ 与 是互为补角;④ 的周长与 边长相等其中正确结论的个数是( )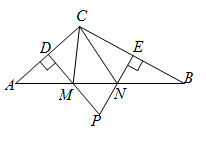 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 若式子 的值存在,则x的取值范围是.14. 计算: .15. 若关于x的不等式组 无解,则m的取值范围是.16. 如图,在等边 中,点D在 边上,点E在 外部,若 , ,连接 , ,则 的形状是.
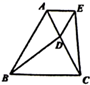 17. 如图,在 中,以点C为圆心, 边的长为半径画弧交 于点D,连接 .若 , ,则 的度数是.
17. 如图,在 中,以点C为圆心, 边的长为半径画弧交 于点D,连接 .若 , ,则 的度数是. 18. 如图,在 中, ,D是 边的中点, 垂直平分 边,动点P在直线 上,若 , ,则线段 的最小值为.
18. 如图,在 中, ,D是 边的中点, 垂直平分 边,动点P在直线 上,若 , ,则线段 的最小值为.
三、解答题
-
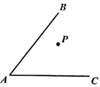
19.(1)、因式分解: ;(2)、利用因式分解计算: .20. 尺规作图(只保留作图痕迹,不要求写出作法及证明过程):如图,已知点P在 内,分别在 、 边上求作点E和点F,使 的周长最小.
 21. 解下列不等式(组),并把它们的解集在数轴上表示出来:(1)、 ;(2)、 .22. 已知: , (n为正整数).(1)、求 的值(结果用含n的代数式表示);(2)、若(1)中代数式的值是整数,求正整数n的最小值.23. 某校为了加强理化生实验操作训练,需购进A,B两种实验标本共75个.已知A种标本的单价为20元,B种标本的单价为12元,若总费用不超过1180元,则最多可以购买多少个A种标本.24. 如图,点O是线段AB的中点,OD∥BC且OD=BC.
21. 解下列不等式(组),并把它们的解集在数轴上表示出来:(1)、 ;(2)、 .22. 已知: , (n为正整数).(1)、求 的值(结果用含n的代数式表示);(2)、若(1)中代数式的值是整数,求正整数n的最小值.23. 某校为了加强理化生实验操作训练,需购进A,B两种实验标本共75个.已知A种标本的单价为20元,B种标本的单价为12元,若总费用不超过1180元,则最多可以购买多少个A种标本.24. 如图,点O是线段AB的中点,OD∥BC且OD=BC.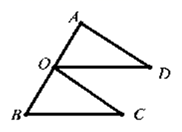 (1)、求证:△AOD≌△OBC;(2)、若∠ADO=35°,求∠DOC的度数.25. 在某市实施城中村改造的过程中,某工程队承包了一项 的拆迁工程.由于准备工作充分,实际拆迁效率比原计划提高了25%,且提前2天完成了任务.(1)、求工程队平均每天实际拆迁的工程量;(2)、为了尽量减少拆迁工作给市民带来的不便,在拆迁了2天后,工程队决定加快推进拆迁工作,确保将余下的拆迁任务在5天内完成,那么工程队平均每天至少再多拆迁的工程量是多少?26. 已知:在等腰 中, ,D是 边的中点,点P在直线 上,点Q在 的延长线上, 是等边三角形.
(1)、求证:△AOD≌△OBC;(2)、若∠ADO=35°,求∠DOC的度数.25. 在某市实施城中村改造的过程中,某工程队承包了一项 的拆迁工程.由于准备工作充分,实际拆迁效率比原计划提高了25%,且提前2天完成了任务.(1)、求工程队平均每天实际拆迁的工程量;(2)、为了尽量减少拆迁工作给市民带来的不便,在拆迁了2天后,工程队决定加快推进拆迁工作,确保将余下的拆迁任务在5天内完成,那么工程队平均每天至少再多拆迁的工程量是多少?26. 已知:在等腰 中, ,D是 边的中点,点P在直线 上,点Q在 的延长线上, 是等边三角形.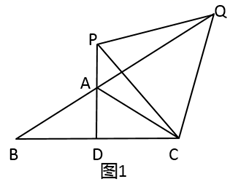
 (1)、如图1,当点P在线段 的延长线上时,求证:
(1)、如图1,当点P在线段 的延长线上时,求证:① ;② ;
(2)、如图2,当点P在线段 上时,(1)中的结论②是否仍然成立?若成立,请说明理由;若不成立,请直接写出线段 , , 三者之间的数量关系.