初中数学浙教版七年级下册第五章 分式 强化提升训练
试卷更新日期:2021-04-18 类型:单元试卷
一、单选题
-
1. 已知三个数 满足 , , ,则 的值是( )A、 B、 C、 D、2. 关于分式 ,当x=-a时,( )A、分式的值为零 B、当 时,分式的值为零 C、分式无意义 D、当a=时,分式无意义3. 下列分式中不是最简分式的是( )A、 B、 C、 D、4. 已知 ,则A的取值是( )A、-3 B、3 C、-6 D、65. 已知:a,b,c三个数满足 ,则 的值为( )A、 B、 C、 D、6. 已知公式 ( ),则表示 的公式是( )A、 B、 C、 D、7. 结论:
①若a + b + c = 0 ,且abc ≠ 0 ,则方程a + bx + c = 0 的解是 x = 1
②若a (x -1) = b(x -1) 有唯一的解,则a ≠b;
③若b = 2a ,则关于 x 的方程ax + b = 0(a ≠ 0)的解为 x = ;
④若a + b + c = 1,且a ≠0 ,则 x = 1一定是方程ax + b + c = 1的解.其中结论正确个数有( ).
A、4个 B、3个 C、2个 D、1个8. 若 是整数,则使分式 的值为整数的 值有( )个.A、2 B、3 C、4 D、59. 关于 的分式方程 的解为正实数,则实数 的取值范围是A、 且 B、 且 C、 且 D、 且10. 学生参加植树造林,甲班每天比乙班多植5棵树,甲班植80棵树与乙班植70棵树所用的天数相等,求甲、乙两班每天各植树多少棵。下面列式错误的是( )A、设甲班每天植树x棵,则 B、设乙班每天植树x棵,则 C、设甲班在x天植树80棵,则 D、设乙班在x天植树70棵,则二、填空题
-
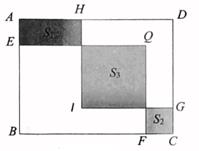
11. 如图,在长方形ABCD中,AB=10,BC=13.E,F,G,H分别是线段AB,BC,CD,AD上的定点.现分别以BE,BF为边作长方形BEQF,以DG为边作正方形DGIH.若长方形BEQF与正方形DGIH的重合部分恰好是一个正方形,且BE=DG,Q,I均在长方形ABCD内部.记图中的阴影部分面积分别为S1 , S2 , S3 . 若 ,则S3= .
 12. 若 ,则 = .13. 如果 对于自然数 成立,则 , .14. 当k=时,方程 会产生增根.15. 某快递公司快递员甲匀速骑车去距公司6000米的某小区取物件,出发几分钟后,该公司快递员乙发现甲的手机落在公司,于是立马匀速骑车去追赶甲,乙出发几分钟后,甲也发现自己的手机落在了公司,立即调头以原速的2倍原路返回,1分钟后遇到了乙,乙把手机给甲后,乙以原速的一半原路返回公司,甲以返回时的速度继续去小区取物件,刚好在事先预计的时间到达该小区.甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示(给手机及中途其它耽误时间忽略不计),则甲到小区时,乙距公司的路程是米.
12. 若 ,则 = .13. 如果 对于自然数 成立,则 , .14. 当k=时,方程 会产生增根.15. 某快递公司快递员甲匀速骑车去距公司6000米的某小区取物件,出发几分钟后,该公司快递员乙发现甲的手机落在公司,于是立马匀速骑车去追赶甲,乙出发几分钟后,甲也发现自己的手机落在了公司,立即调头以原速的2倍原路返回,1分钟后遇到了乙,乙把手机给甲后,乙以原速的一半原路返回公司,甲以返回时的速度继续去小区取物件,刚好在事先预计的时间到达该小区.甲、乙两人相距的路程y(米)与甲出发的时间x(分钟)之间的关系如图所示(给手机及中途其它耽误时间忽略不计),则甲到小区时,乙距公司的路程是米.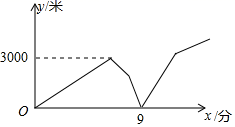 16. 已知实数 满足 ,则 .
16. 已知实数 满足 ,则 .三、综合题
-
17.(1)、计算:(2)、18. 解分式方程(1)、(2)、19. 阅读材料:
关于x的方程: 的解是 , ;
(即 )的解是 ;
的解是 , ;
的解是 , ;……
(1)、请观察上述方程与解的特征,比较关于x的方程 与它们的关系,猜想它的解是什么?并利用“方程的解”的概念进行验证。(2)、由上述的观察、比较、猜想、验证,可以得出结论:如果方程的左边是未知数与其倒数的倍数的和,方程的右边的形式与左边完全相同,只是把其中的未知数换成了某个常数,那么这样的方程可以直接得解,请用这个结论解关于x的方程: 。
20. 某市为了做好“全国文明城市”验收工作,计划对市区 米长的道路进行改造,现安排甲、乙两个工程队进行施工.(1)、已知甲工程队改造360米的道路与乙工程队改造300米的道路所用时间相同.若甲工程队每天比乙工程队多改造30米,求甲、乙两工程队每天改造道路的长度各是多少米.(2)、若甲工程队每天可以改造 米道路,乙工程队每天可以改造 米道路,(其中 ).现在有两种施工改造方案:方案一:前 米的道路由甲工程队改造,后 米的道路由乙工程队改造;
方案二:完成整个道路改造前一半时间由甲工程队改造,后一半时间由乙工程队改造.
根据上述描述,请你判断哪种改造方案所用时间少?并说明理由.
21. 张康和李健两名运动爱好者周末相约到丹江环库绿道进行跑步锻炼.(1)、周日早上 点,张康和李健同时从家出发,分别骑自行车和步行到离家距离分别为 千米和 千米的绿道环库路入口汇合,结果同时到达,且张康每分钟比李健每分钟多行 米,求张康和李健的速度分别是多少米 分?(2)、两人到达绿道后约定先跑 千米再休息,李健的跑步速度是张康跑步速度的 倍,两人在同起点,同时出发,结果李健先到目的地 分钟.①当 , 时,求李健跑了多少分钟?
②求张康的跑步速度多少米 分?(直接用含 , 的式子表示)
22. 姐妹两人在50米的跑道上进行短路比赛,两人从出发点同时起跑,姐姐到达终点时,妹妹离终点还差3米,已知姐妹两人的平均速度分别为a米/秒、b米/秒.(1)、如果两人重新开始比赛,姐姐从起点向后退3米,姐妹同时起跑,两人能否同时到达终点?若能,请求出两人到达终点的时间;若不能,请说明谁先到达终点.(2)、如果两人想同时到达终点,应如何安排两人的起跑位置?请你设计两种方案.23. 周日琪琪要骑车从家去书店买书,一出家门,遇到了邻居亮亮,亮亮说:“今天有风,而且去时逆风,要吃亏了”,琪琪回答说:“去时逆风,回来时顺风,和无风往返一趟所用时间相同”.(顺风速度 无风时骑车速度 风速,逆风速度 无风时骑车速度 风速)(1)、如果家到书店的路程是 ,无风时琪琪骑自行车的速度是 ,他逆风去书店所用时间是顺风回家所用时间的 倍,求风速是多少?(2)、如果设从家到书店的路程为 千米,无风时骑车速度为 千米/时,风速为 千米/时 ,求出有风往返一趟的时间,无风往返一趟的时间,请你通过计算说明琪琪和亮亮谁说得对.24. 阅读下列材料:【材料1】我们知道,假分数可以化为整数与真分数的和的形式,例如: =1+ 。在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为假分式;当分子的次数小于分母的次数时,我们称之为真分式,如 , ,…这样的分式是假分式;如 与 …这样的分式是真分式。类似的,假分式也可以化为整式与真分式的和(差)的形式。
例如:将分式 化成一个整式与一个真分式的和(差)的形式。
方法1: = = =x-1-
方法2:由分母为x+3,可设x2+2x-5=(x+3)(x+a)+b(a,b为待确定的系数)
∵(x+3)(x+a)+b=x2+ax+3x+3a+b=x²+(a+3)x+(3a+b)
∴x²+2x-5=x²+(a+3)x+(3a+b)
对于任意x,上述等式均成立,
∴ ,解得
∴x²+2x-5=(x+3)(x-1)-2
∴ = = =x-1-
这样,分式 就被化成一个整式与一个真分式的和(差)的形式。
【材料2】对于式子2+ ,由x2≥0知1+x²的最小值为1,所以 的最大值为3,
所以2+ 的最大值为5。
请根据上述材料,解答下列问题:
(1)、分式 是分式(填“真”或“假”)。(2)、把下列假分式化成一个整式与一个真分式的和(差)的形式:① =+。
② =+。
(3)、把分式 化成一个整式与一个真分式的和(差)的形式,并求x取何整数时,这个分式的值为整数。(4)、当x的值变化时,求分式 的最大值。