初中数学湘教版七年级下册第四章相交线与平行线 强化提升训练
试卷更新日期:2021-04-17 类型:单元试卷
一、单选题
-
1. 下列说法正确的是( )A、同一平面内不相交的两线段必平行 B、同一平面内不相交的两射线必平行 C、同一平面内不相交的一条线段与一条直线必平行 D、同一平面内不相交的两条直线必平行2. 观察图形,下列说法正确的个数是( )
(1)直线BA和直线AB是同一条直线;(2)AB+BD>AD;(3)射线AC和射线AD是同一条射线;(4)三条直线两两相交时,一定有三个交点 A、1个 B、2个 C、3个 D、4个3. 平面上三条直线两两相交最多能构成对顶角的对数是( ).A、7 B、6 C、5 D、44. 如图所示,由△ABC平移得到的三角形的个数是( )
A、1个 B、2个 C、3个 D、4个3. 平面上三条直线两两相交最多能构成对顶角的对数是( ).A、7 B、6 C、5 D、44. 如图所示,由△ABC平移得到的三角形的个数是( )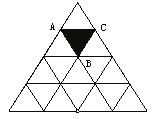 A、5 B、15 C、8 D、65. 已知n(n≥3,且n为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当n=3时,共有2个交点;当n=4时,共有5个交点;当n=5时,共有9个交点;…依此规律,当共有交点个数为27时,则n的值为( )
A、5 B、15 C、8 D、65. 已知n(n≥3,且n为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当n=3时,共有2个交点;当n=4时,共有5个交点;当n=5时,共有9个交点;…依此规律,当共有交点个数为27时,则n的值为( )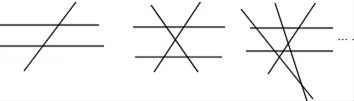 A、6 B、7 C、8 D、96. 如图,长方形ABCD中,AB=8,第一次平移长方形ABCD沿AB的方向向右平移6个单位,得到长方形A1B1C1D1 , 第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移6个单位,得到长方形A2B2C2D2 , ……第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1的方向平移6个单位,得到长方形AnBn∁nDn(n>2),若ABn的长度为2018,则n的值为( )
A、6 B、7 C、8 D、96. 如图,长方形ABCD中,AB=8,第一次平移长方形ABCD沿AB的方向向右平移6个单位,得到长方形A1B1C1D1 , 第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移6个单位,得到长方形A2B2C2D2 , ……第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1的方向平移6个单位,得到长方形AnBn∁nDn(n>2),若ABn的长度为2018,则n的值为( ) A、334 B、335 C、336 D、3377. 如图,AB∥EF,∠ABP= ∠ABC,∠EFP= ∠EFC,已知∠FCD=60°,则∠P的度数为( )
A、334 B、335 C、336 D、3377. 如图,AB∥EF,∠ABP= ∠ABC,∠EFP= ∠EFC,已知∠FCD=60°,则∠P的度数为( ) A、60° B、80° C、90° D、100°8. 如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )
A、60° B、80° C、90° D、100°8. 如图所示,OA⊥OC,OB⊥OD,下面结论中,其中说法正确的是( )
①∠AOB=∠COD;②∠AOB+∠COD=90°;③∠BOC+∠AOD=180°;④∠AOC-∠COD=∠BOC.
A、①②③ B、①②④ C、①③④ D、②③④9. 如图 ,若 表示三角形 的面积, 表示三角形 的面积,则下列结论正确的是( )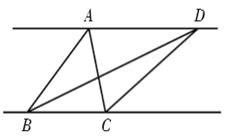 A、 B、 C、 D、10. ①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )
A、 B、 C、 D、10. ①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )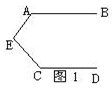


 A、、1个 B、2个 C、3个 D、4个
A、、1个 B、2个 C、3个 D、4个二、填空题
-
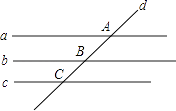
11. 有4条直线a、b、c、d以及3个交点A、B、C,在图中画出的部分可以数出对同位角.
 12.
12.如图,是一块从一个边长为20cm的正方形BCDM材料中剪出的垫片,经测得FG=9cm,则这个剪出的图形的周长是cm.
 13. 已知∠A与∠B(∠A,∠B都是大于0°且小于180°的角)的两边一边平行,另一边垂直,且2∠A-∠B=18°,则∠A的度数为。14. 一副直角三角尺如图①叠放,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图②,当∠BAD=15°时,有一组边BC∥DE,请再写出两个符合要求的∠BAD(0°<∠BAD<180°)的度数.
13. 已知∠A与∠B(∠A,∠B都是大于0°且小于180°的角)的两边一边平行,另一边垂直,且2∠A-∠B=18°,则∠A的度数为。14. 一副直角三角尺如图①叠放,现将45°的三角尺ADE固定不动,将含30°的三角尺ABC绕顶点A顺时针转动,要求两块三角尺的一组边互相平行.如图②,当∠BAD=15°时,有一组边BC∥DE,请再写出两个符合要求的∠BAD(0°<∠BAD<180°)的度数.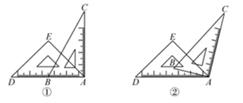 15. 在间一平面内,有2019条互不重合的直线,l1 , l2 , l3 , …,l2019 , 若l1⊥l2 , l2∥l3 , l3⊥l4 , l4∥l5 , 以此类推,则l1和l2019的位置关系是.16. 如图,已知直线m//n,A,B 为直线m上的两点,C,P 为直线n上的两点.
15. 在间一平面内,有2019条互不重合的直线,l1 , l2 , l3 , …,l2019 , 若l1⊥l2 , l2∥l3 , l3⊥l4 , l4∥l5 , 以此类推,则l1和l2019的位置关系是.16. 如图,已知直线m//n,A,B 为直线m上的两点,C,P 为直线n上的两点.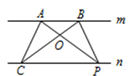 (1)、请写出图中面积相等的各对三角形:;(2)、如果A,B,C 为三个定点,点P 在直线n上移动,那么,无论P 点移动到任何位置,总有 .
(1)、请写出图中面积相等的各对三角形:;(2)、如果A,B,C 为三个定点,点P 在直线n上移动,那么,无论P 点移动到任何位置,总有 .理由是: .
三、解答题
-
17. 平面上有7条不同的直线,如果其中任何三条直线都不共点.(1)、请画出满足上述条件的一个图形,并数出图形中各直线之间的交点个数;(2)、请再画出各直线之间的交点个数不同的图形(至少两个);(3)、你能否画出各直线之间的交点个数为n的图形,其中n分别为6,21,15?(4)、请尽可能多地画出各直线之间的交点个数不同的图形,从中你能发现什么规律?18. 如图 ,AB∥CD,且∠PMQ=2∠QMB,∠PNQ=2∠QND,判断∠P 与∠Q的数量关系,并说明理由.
 19. 如图,将直角△ABC(AC为斜边)沿直角边AB方向平移得到直角△DEF,已知BE=6,EF=10,CG=3,求阴影部分的面积.
19. 如图,将直角△ABC(AC为斜边)沿直角边AB方向平移得到直角△DEF,已知BE=6,EF=10,CG=3,求阴影部分的面积. 20. 在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的顶点都在正方形网格的格点(网格线的交点)上.
20. 在如图所示的正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的顶点都在正方形网格的格点(网格线的交点)上. (1)、画出△ABC先向右平移5个单位长度,再向上平移2个单位长度所得的△A1B1C1;
(1)、画出△ABC先向右平移5个单位长度,再向上平移2个单位长度所得的△A1B1C1;
画出△ABC的中线AD,标出点D;
画出△ABC的AC边上的高线BE所在直线,标出垂足E;(要求只能通过连接格点方式作图).(2)、在(1)的条件下,线段AA1和CC1的关系是.(3)、画一个△ABP(要求各顶点在格点上,P不与C点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共个.21. 复杂的数学问题我们常会把它分解为基本问题来研究,化繁为简,化整为零这是一种常见的数学解题思想. (1)、如图1,直线 , 被直线 所截,在这个基本图形中,形成了对同旁内角.(2)、如图2,平面内三条直线 , , 两两相交,交点分别为A、B、C,图中一共有对同旁内角.(3)、平面内四条直线两两相交,最多可以形成对同旁内角.(4)、平面内n条直线两两相交,最多可以形成对同旁内角.22. 已知:如图1,AB∥CD,点E,F分别为AB,CD上一点.
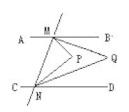
(1)、如图1,直线 , 被直线 所截,在这个基本图形中,形成了对同旁内角.(2)、如图2,平面内三条直线 , , 两两相交,交点分别为A、B、C,图中一共有对同旁内角.(3)、平面内四条直线两两相交,最多可以形成对同旁内角.(4)、平面内n条直线两两相交,最多可以形成对同旁内角.22. 已知:如图1,AB∥CD,点E,F分别为AB,CD上一点.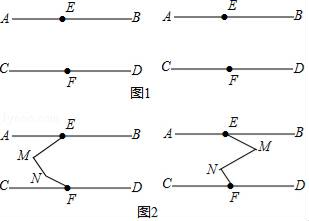 (1)、在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系.请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明;(2)、如图2,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).23. 如图 ,已知直线l1 , l2 , 点P在直线l3上且不与点A、B重合.记∠AEP=∠1,∠BFP=∠2,∠EPF=∠3.
(1)、在AB,CD之间有一点M(点M不在线段EF上),连接ME,MF,试探究∠AEM,∠EMF,∠MFC之间有怎样的数量关系.请补全图形,并在图形下面写出相应的数量关系,选其中一个进行证明;(2)、如图2,在AB,CD之间有两点M,N,连接ME,MN,NF,请选择一个图形写出∠AEM,∠EMN,∠MNF,∠NFC 存在的数量关系(不需证明).23. 如图 ,已知直线l1 , l2 , 点P在直线l3上且不与点A、B重合.记∠AEP=∠1,∠BFP=∠2,∠EPF=∠3. (1)、如图 ,若直线l1//l2 , 点P在线段AB(A、B两点除外)上运动时,写出∠1、∠2、∠3之间的关系,并说明理由.(2)、如图 ,若(1)中∠1、∠2、∠3之间的关系成立,你能不能反向推出直线l1//l2?若成立请说明理由.(3)、如图 ,若直线l1//l2 , 若点P在A、B两点外侧运动时(不包括线段AB),请直接写出∠1、∠2、∠3之间的关系.24. 如图
(1)、如图 ,若直线l1//l2 , 点P在线段AB(A、B两点除外)上运动时,写出∠1、∠2、∠3之间的关系,并说明理由.(2)、如图 ,若(1)中∠1、∠2、∠3之间的关系成立,你能不能反向推出直线l1//l2?若成立请说明理由.(3)、如图 ,若直线l1//l2 , 若点P在A、B两点外侧运动时(不包括线段AB),请直接写出∠1、∠2、∠3之间的关系.24. 如图 (1)、图中,∠ABC的两边和∠DEF的两边分别互相平行,既AB∥DE,BC∥EF,试说明∠ABC=∠DEF.(2)、一个角的两边分别平行于另一个角的两边,除了图1中相等情形外,是否存在其他不相等情形,探究此情形下两个角的关系(画出图形,写出结论并说明理由).(3)、如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?(画出图形,直接写出结论)(4)、如果一个角的两边和另一个角的两边,其中一边互相平行,另一边互相垂直,则这两个角是什么关系?(画出图形,直接写出结论)
(1)、图中,∠ABC的两边和∠DEF的两边分别互相平行,既AB∥DE,BC∥EF,试说明∠ABC=∠DEF.(2)、一个角的两边分别平行于另一个角的两边,除了图1中相等情形外,是否存在其他不相等情形,探究此情形下两个角的关系(画出图形,写出结论并说明理由).(3)、如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?(画出图形,直接写出结论)(4)、如果一个角的两边和另一个角的两边,其中一边互相平行,另一边互相垂直,则这两个角是什么关系?(画出图形,直接写出结论)