初中数学湘教版七年级下册4.5垂线 同步练习
试卷更新日期：2021-04-17 类型：同步测试
一、单选题
-
1. 点P为直线l外一点，点A，B，C在直线l上，若 ， ， ，则点P到直线l的距离是（ ）A、 B、 C、不大于 D、2. 下列说法正确的个数是（ ）
①射线 与射线 是同一条射线；②点 到点 的距离是线段 ；③画一条长为 的直线；④在同一平面内，过一点有且只有一条直线垂直于已知直线.
A、0个 B、1个 C、2个 D、3个3. 如图，直线a∥b，点B在直线b上，AB⊥BC， ，则 （ ）
A、35° B、45° C、55° D、25°4. 如图，连接直线 外一点 与直线 上各点 ， ，其中 ，这些线段 ， ， ， ， 中，最短的线段是（ ）
A、 B、 C、 D、5. 如图.直线a∥b，直线L与a、b分别交于点A，B，过点A作AC⊥b于点C.若∠1＝50°，则∠2的度数为（ ）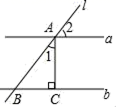
A、130° B、50° C、40° D、25°6. 点 为直线 外一点，点 为直线 上三点， ，则点到直线 的距离为（ ）A、 B、 C、 D、不大于7. 在同－平面内，若∠A与∠B的两边分别垂直，且∠A比∠B的3倍少40°，则∠A的度数为（ ）A、20° B、55° C、20°或 125° D、20°或55°8. 如图，在立定跳远中，体育老师是这样测量运动员的成绩的，用一块直角三角板的一边附在起跳线上，另一边与拉直的皮尺重合，这样做的理由（ ）
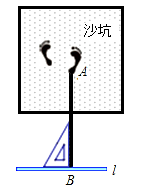A、垂线段最短 B、过两点有且只有一条直线 C、过一点可以作无数条直线 D、两点之间线段最短9. 如图，直线AB，CD相交于点O，下列条件中：①∠AOD＝90° ；②∠AOD＝∠AOC；③∠AOC+∠BOC＝180°；④∠AOC+∠BOD＝180°，能说明AB⊥CD的有（ ）
A、1个 B、2个 C、3个 D、4个10. 如图，三角形ABC中，∠C＝90°，AC＝3，点P是BC边上一动点，则AP的长不可能是（ ）
A、3 B、2.8 C、3.5 D、4二、填空题
-
11. 如图，△ABC中，∠ACB=90°，CD⊥AB于点D，则点B到直线CD的距离是线段的长．
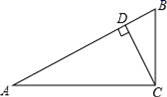12. 如图，已知a∥b，AC⊥AB，AC交直线b于点C，∠1＝65°，那么∠2的度数为.
13. 如图，线段AB=15cm ， 线段AD=12cm ， 线段AC=9cm ， 则点A到BC的距离为 cm ．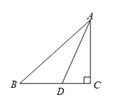
14. 如图，已知AE//CD，BC⊥CD于C，若∠A＝28°，则∠ABC＝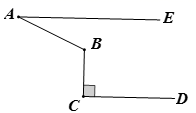
三、解答题
-
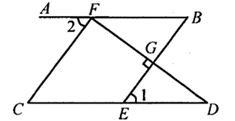
15. 已知：如图，DG⊥BC，AC⊥BC，EF⊥AB，∠1＝∠2，求证：CD⊥AB.
证明：∵DG⊥BC，AC⊥BC（已知）
∴∠DGC＝∠ACB＝90°（ ）
∴∠DGC+∠ACB＝180°
∴▲∥▲（ ）
∴∠2＝▲（ ）
∵∠1＝∠2（已知）
∴∠1＝▲（ ）
∴EF∥CD （ ）
∴∠AEF＝▲（ ）
∵EF⊥AB （ ）
∴∠AEF＝90°
∴∠ADC＝90°
∴CD⊥AB.
16. 如图，在△ABC中，点E、H在BC上，EF⊥AB，HD⊥AB，垂足分别是F、D，点G在AC上，∠AGD＝∠ACB，试说明∠1+∠2＝180°.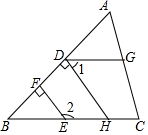
17. 如图，平面内有三个点A，B，C，请你根据下列要求完成作图(作图工具不限)
①画直线AB，射线CB，线段AC；
②过点C作直线l⊥直线AB，垂足为D。
