初中数学湘教版七年级下册4.1.1相交与平行 同步练习

试卷更新日期：2021-04-17 类型：同步测试

进入 出卷网 下载

一、单选题

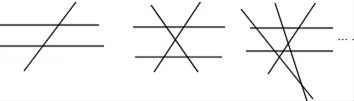
  • 1. 在同一平面内，两条不重合的直线的位置关系可能是（   ）
    A、平行或相交 B、垂直或相交 C、垂直或平行 D、平行、垂直或相交

    查看试题解析

  • 2. 在同一平面内，两条不重合的直线的位置关系是 ( 　　 )
    A、平行 B、相交 C、相交或平行 D、垂直

    查看试题解析

  • 3. 如果 a//b ， b//c ，那么 a//c ，这个推理的依据是 (   )
    A、等量代换 B、两直线平行，同位角相等 C、平行公理 D、平行于同一直线的两条直线平行

    查看试题解析

  • 4. a ， b ， c 是同一平面内的三条直线，下列说法错误的是（    ）
    A、如果 a∥b ， b∥c ，那么 a∥c B、如果 a∥b ， b⊥c ，那么 a⊥c C、如果 a⊥c ， b⊥c ，那么 a⊥c D、如果 a⊥b ， b⊥c ，那么 a∥c

    查看试题解析

  • 5. 若P，Q是直线AB外不重合的两点，则下列说法不正确的是（   ）
    A、直线PQ可能与直线AB垂直 B、直线PQ可能与直线AB平行 C、过点P的直线一定能与直线AB相交 D、过点Q只能画出一条直线与AB平行

    查看试题解析

  • 6. 下列说法中，正确的是（   ）
    A、在同一平面内，两条直线的位置关系只有相交，平行两种 B、在同一平面内，不相交的两条线段互相平行 C、在同一平面内，不相交的两条直线互相平行 D、在同一平面内，不相交的两条射线互相平行

    查看试题解析

  • 7. 平面内有三条直线，那么它们的交点个数有（   ）
    A、0个或1个 B、0个或2个 C、0个或1个或2个 D、0个或1个或2个或3个

    查看试题解析

  • 8. 已知n（n≥3，且n为整数）条直线中只有两条直线平行，且任何三条直线都不交于同一个点．如图，当n=3时，共有2个交点；当n=4时，共有5个交点；当n=5时，共有9个交点；…依此规律，当共有交点个数为27时，则n的值为（     ）

    A、6 B、7 C、8 D、9

    查看试题解析

二、填空题

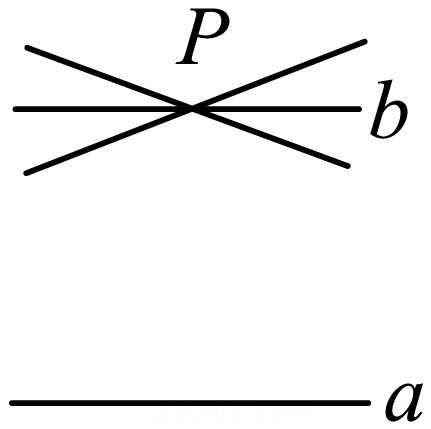
  • 9. 同一平面内两条直线若相交，则公共点的个数为个

    查看试题解析

  • 10. 直线l的同侧有A，B，C三点，如果A，B两点确定的直线l1与B，C两点确定的直线l2都与l平行，那么A，B，C三点在同一条直线上，理由是

    查看试题解析

  • 11. 如图，在直线a外有一点P，经过点P可以画无数条直线，如果 a//b ，那么过点P的其它直线与直线a一定不平行，理由是 ．

    查看试题解析

  • 12. 平面内两两相交的三条直线，如果它们最多有a个交点，最少有b个交点，则a+b＝ ．

    查看试题解析

三、解答题

  • 13. 简单应用．将一张长方形纸片对折两次，得到三条折痕，这三条折痕有什么关系，请说明理由即可．

    查看试题解析

  • 14. 生活中可找出许许多多平行线的实例，如课桌的对边等，你再找找这种实例，同学们互相交流交流．

    查看试题解析

  • 15. 已知平面上四点A，B，C，D，如图：

    (1)、请按要求画图：①画直线AB，射线CD；②画射线AD，连接BC；③直线AB与射线CD相交于E；④连接AC、BD相交于点F.
    (2)、根据以上作图，请判断下列位置关系：①点C与直线AB；②点E与直线CD；③直线AB与直线CD.

    查看试题解析

  • 16. 根据下列要求画图．

    (1)、如图(1)所示，过点A画MN∥BC；
    (2)、如图(2)所示，过点P画PE∥OA，交OB于点E，过点P画PH∥OB，交OA于点H；

    (3)、如图(3)所示，过点C画CE∥DA，与AB交于点E，过点C画CF∥DB，与AB的延长线交­于点F．

    查看试题解析