初中数学浙教版七年级下册4.3 用乘法公式分解因式同步练习

试卷更新日期：2021-04-17 类型：同步测试

进入出卷网下载

一、单选题

1. 若x²+mx+9＝（x﹣3）² ，则m的值为（）

A、6 B、﹣6 C、±6 D、3

查看试题解析
2. 多项式y²－my＋144成为完全平方式，则m的值为（）

A、 $\pm$ 12 B、24 C、±24 D、12

查看试题解析
3. 将多项式 $x^{3} - x y^{2}$ 分解因式，结果正确的是（）

A、 $x (x^{2} - y^{2})$ B、 $x {(x - y)}^{2}$ C、 $x {(x + y)}^{2}$ D、 $x (x + y) (x - y)$

查看试题解析
4. 下列多项式中，是完全平方式的为（）

A、 $x^{2} - x + \frac{1}{4}$ B、 $x^{2} + \frac{1}{2} x + \frac{1}{4}$ C、 $x^{2} + \frac{1}{4} x - \frac{1}{4}$ D、 $x^{2} - \frac{1}{4} x + \frac{1}{4}$

查看试题解析
5. 将多项式 $4 x^{2} + 1$ 加上一个单项式后，使它能成为一个完全平方式，下列添加单项式错误的是（）

A、 $2 x$ B、 $4 x$ C、 $- 4 x$ D、 $4 x^{4}$

查看试题解析
6. 下列分解因式正确的是（）

A、 $x^{2} + 2 x y - y^{2} = {(x - y)}^{2}$ B、 $3 a x^{2} - 6 a x = 3 (a x^{2} - 2 a x)$ C、 $m^{3} - m = m (m - 1) (m + 1)$ D、 $a^{2} - 4 = {(a - 2)}^{2}$

查看试题解析
7. 小明在利用完全平方公式计算一个二项整式的平方时，不小心用墨水把中间一项的系数染黑了，得到正确的结果为4a²■ab+9b² ，则中间一项的系数是（）

A、12 B、﹣12 C、12或﹣12 D、36

查看试题解析
8. 下列各式中：① $- x^{2} - y^{2} = - (x + y) (x - y)$ ，② $- x^{2} + y^{2} = (- x + y) (x + y)$ ， ③ $x^{2} - 2 x - 4 = {(x - 2)}^{2}$ ，④ $x^{2} + x + \frac{1}{4} = {(x + \frac{1}{2})}^{2}$ 中，分解因式正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 已知 $x^{2} - m x + 9$ 是某个整式的平方的展开式，则m 的值为（）

A、3 B、±3 C、6 D、±6

查看试题解析
10. 下列多项式能用平方差公式分解因式的是（）

A、 $x^{2} - x y$ B、 $x^{2} + x y$ C、 $4 x^{2} + y^{2}$ D、 $4 x^{2} - y^{2}$

查看试题解析

二、填空题

11. 分解因式：x³﹣25x＝.

查看试题解析
12. 若 $a + b = 3$ ， $a b = 2$ ，则 ${(a - b)}^{2} =$ .

查看试题解析
13. 在括号中填上适当的数，使等式成立： $x^{2} - 2 x + 1 = (x -$ ）² .

查看试题解析
14. 将多项式x²+4加上一个单项式，使它成为完全平方式，这个单项式可能是(写出一个即可)

查看试题解析
15. 在实数范围内分解因式： x²+4x+1

查看试题解析

三、解答题

16. 因式分解：

(1)、 $4 x^{2} - 8 x y + 2 x$

(2)、 $3 x (a - b) - 6 y (b - a)$

(3)、 $2 a^{3} - 8 a$

(4)、 ${(x^{2} + 4)}^{2} - 16 x^{2}$

查看试题解析
17. 因式分解

(1)、 $2 a b - 4 b$ ；

(2)、 $3 x y^{3} - 6 x^{2} y^{2} + 3 x^{3} y^{}$ ；

(3)、 $m^{2} (7 - m) + 9 (m - 7)$ ．

查看试题解析
18. 请你说明：m（m+1）（m+2）（m+3）+1是一个完全平方式．

查看试题解析
19. 下面是小华同学分解因式 $9 a^{2} (x - y) + 4 b^{2} (y - x)$ 的过程，请认真阅读，并回答下列问题．
解：原式 $= 9 a^{2} (x - y) + 4 b^{2} (x - y)$ ①

$= (x - y) (9 a^{2} + 4 b^{2})$ ②

$= (x - y) {(3 a + 2 b)}^{2}$ ③

任务一：以上解答过程从第步开始出现错误．

任务二：请你写出正确的解答过程．

查看试题解析
20. 已知多项式(a²+ka+25)–b² ，在给定k的值的条件下可以因式分解即：前半部分可以写成完全平方公式

(1)、写出常数k可能给定的值；

(2)、针对其中一个给定的k值，写出因式分解的过程.

查看试题解析
21. 已知a，b，c是 $△ A B C$ 的三边，且满足 $a^{2} - b^{2} + a c - b c = 0$ ，试判断 $△ A B C$ 的形状，并说明理由．

查看试题解析
22. 已知二次三项式x²+px+q的常数项与（x-1）（x-9）的常数项相同，而它的一次项与（x-2）（x-4）的一次项相同，试将此多项式因式分解．

查看试题解析
23. 阅读以下材料，并按要求完成相应的任务．
在初中数学课本中重点介绍了提公因式法和运用公式法两种因式分解的方法，其中运用公式法即运用平方差公式：a²-b²=（a+b）（a-b）和完全平方公式：a²±2ab+b²=（a±b）²进行分解因式，能运用完全平方公式分解因式的多项式必须是三项式，其中有两项能写成两个数（或式）的平方和的形式，另一项是这两个数（或式）的积的2倍．当一个二次三项式不能直接运用完全平方公式分解因式时，可应用下面方法分解因式，先将多项式ax²+bx+c（a≠0）变形为a（x+m）²+n的形式，我们把这样的变形方法叫做多项式ax²+bx+c的配方法．再运用多项式的配方法及平方差公式能对一些多项式进行分解因式．

例如：x²+8x+7

=x²+8x+16-16+7

=（x+4）²-9

=（x+4+3）（x+4-3）

=（x+7）（x+1）

根据以上材料，完成相应的任务：

(1)、利用“多项式的配方法”将x²+2x-3化成a（x+m）²+n的形式为；

(2)、请你利用上述方法因式分解：
①x²+6x+8；

②x²-6x-7．

查看试题解析
24. 将两个大小不一的等腰直角三角形按如图①，②的方式摆放，设两个三角形的直角边长分别为 $x$ ， $y (x > y > 0)$ ，图②中阴影部分的面积为 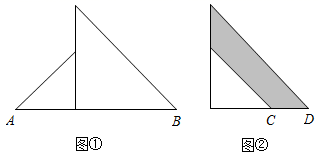$S$ .

(1)、用含 $x$ ， $y$ 的代数式表示图②中阴影部分的面积；

(2)、将（1）中的代数式因式分解；

(3)、若 $A B = a$ ， $C D = b$ ，用含 $a$ ， $b$ 的式子表示图②中阴影部分的面积.

查看试题解析

初中数学浙教版七年级下册4.3 用乘法公式分解因式 同步练习

一、单选题

二、填空题

三、解答题

初中数学浙教版七年级下册4.3 用乘法公式分解因式同步练习