初中数学浙教版八年级下册第四章 平行四边形 强化提升训练
试卷更新日期:2021-04-17 类型:单元试卷
一、单选题
-
1. 如图,∠A+∠B+∠C+∠D+∠E+∠F的度数为( )
 A、180° B、360 C、270° D、540°2. 如图,在边长为1的正六边形 中,M是边 上一点,则线段 的长可以是( )
A、180° B、360 C、270° D、540°2. 如图,在边长为1的正六边形 中,M是边 上一点,则线段 的长可以是( ) A、1.4 B、1.6 C、1.8 D、2.23.
A、1.4 B、1.6 C、1.8 D、2.23.如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PMN的面积;③△PAB的周长;④∠APB的大小;⑤直线MN,AB之间的距离.其中会随点P的移动而不改变的是( )
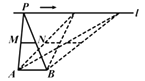 A、①②③ B、①②⑤ C、②③④ D、②④⑤4. 如图所示的方格纸上有一平行四边形ABCD,其顶点均在网格线的交点上,且E点在AD上.今大华在方格纸网格线的交点上任取一点F,发现△FBC的面积比△EBC的面积大.判断下列哪一个图形可表示大华所取F点的位置?( )
A、①②③ B、①②⑤ C、②③④ D、②④⑤4. 如图所示的方格纸上有一平行四边形ABCD,其顶点均在网格线的交点上,且E点在AD上.今大华在方格纸网格线的交点上任取一点F,发现△FBC的面积比△EBC的面积大.判断下列哪一个图形可表示大华所取F点的位置?( )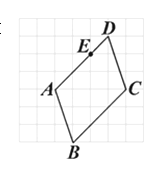 A、
A、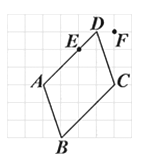 B、
B、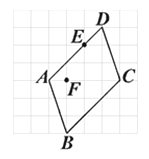 C、
C、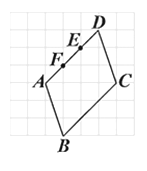 D、
D、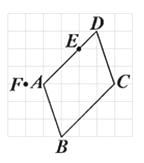 5. 如图,点O是 的对称中心, ,E、F是 边上的点,且 ;G、H是 边上的点,且 ,若 分别表示 和 的面积,则 与 之间的等量关系是( )
5. 如图,点O是 的对称中心, ,E、F是 边上的点,且 ;G、H是 边上的点,且 ,若 分别表示 和 的面积,则 与 之间的等量关系是( )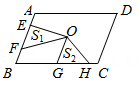 A、 B、 C、 D、6. 如图,已知 ABCD三个顶点坐标是A(-1,0) 、B(-2,-3) 、C(2,-1) ,那么第四个顶点D的坐标是( )
A、 B、 C、 D、6. 如图,已知 ABCD三个顶点坐标是A(-1,0) 、B(-2,-3) 、C(2,-1) ,那么第四个顶点D的坐标是( )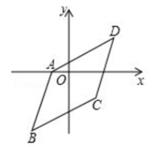 A、(3,1) B、(3,2) C、(3,3) D、(3,4)7. 如图所示,已知△ABC与△CDA关于点O对称,过O作EF分别交AD,BC于点E,F,下面的结论:①点E和点F,点B和点D是关于点O的对应点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称,其中正确的有( )
A、(3,1) B、(3,2) C、(3,3) D、(3,4)7. 如图所示,已知△ABC与△CDA关于点O对称,过O作EF分别交AD,BC于点E,F,下面的结论:①点E和点F,点B和点D是关于点O的对应点;②直线BD必经过点O;③四边形ABCD是中心对称图形;④四边形DEOC与四边形BFOA的面积必相等;⑤△AOE与△COF成中心对称,其中正确的有( )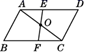 A、1个 B、2个 C、3个 D、5个8. 如图,在四边形 中, , , ,E是 的中点.点P以每秒1个单位长度的速度从点A出发,沿 向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿 向点B运动.点P停止运动时,点Q也随之停止运动.若以点 为顶点的四边形是平行四边形,则点P运动的时间为( )
A、1个 B、2个 C、3个 D、5个8. 如图,在四边形 中, , , ,E是 的中点.点P以每秒1个单位长度的速度从点A出发,沿 向点D运动;点Q同时以每秒3个单位长度的速度从点C出发,沿 向点B运动.点P停止运动时,点Q也随之停止运动.若以点 为顶点的四边形是平行四边形,则点P运动的时间为( )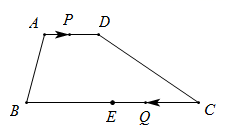 A、1 B、 C、2或 D、1或9. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OA,OB,CD的中点,EG交FD于点H.则下列结论:①ED⊥CA;②EF=CG;③EH= EG;④S△EFD=S△CEG成立的个数有( )
A、1 B、 C、2或 D、1或9. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,BD=2AD,E,F,G分别是OA,OB,CD的中点,EG交FD于点H.则下列结论:①ED⊥CA;②EF=CG;③EH= EG;④S△EFD=S△CEG成立的个数有( ) A、1个 B、2个 C、3个 D、4个10. 用反证法证明“在三角形中,至少有一个内角大于或等于60°”时,应先假设( )A、在三角形中,三个内角都大于60° B、在三角形中,三个内角都小于60° C、在三角形中,至少有一个内角大于60° D、在三角形中,至少有一个内角小于60°
A、1个 B、2个 C、3个 D、4个10. 用反证法证明“在三角形中,至少有一个内角大于或等于60°”时,应先假设( )A、在三角形中,三个内角都大于60° B、在三角形中,三个内角都小于60° C、在三角形中,至少有一个内角大于60° D、在三角形中,至少有一个内角小于60°二、填空题
-
11. 过四边形的一个顶点可以画一条对角线,且把四边形分成两个三角形;过五边形的一个顶点可以画两条对角线,且把五边形分成三个三角形;......猜想:过n边形的一个顶点可以画条对角线,且把n边形分成 个三角形.12. 在 中, 边上的高为4, , ,则 的周长等于.13. 如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为 .
 14. 如图四边形ABCD , AD∥BC , AB⊥BC , AD=1,AB=2,BC=3,P为AB边上的一动点,以PD , PC为边作平行四边形PCQD , 则对角线PQ的长的最小值是.
14. 如图四边形ABCD , AD∥BC , AB⊥BC , AD=1,AB=2,BC=3,P为AB边上的一动点,以PD , PC为边作平行四边形PCQD , 则对角线PQ的长的最小值是. 15. 如图所示的三角形纸片中, , BC=12cm, ,折叠这个三角形,使点B落在AC的中点D处,折痕为EF,那么BF的长为cm.
15. 如图所示的三角形纸片中, , BC=12cm, ,折叠这个三角形,使点B落在AC的中点D处,折痕为EF,那么BF的长为cm. 16. 用一个值a说明命题“若ax>a,则x>1”是不正确的,则a的值可以是 .
16. 用一个值a说明命题“若ax>a,则x>1”是不正确的,则a的值可以是 .三、综合题
-
17. 设a,b,c是不全相等的任意整数,若x=a2-bc,y=b2-ac,z=c2-ab.求证:x,y,z中至少有一个大于零.
18. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后, 的顶点均在格点上,点 的坐标为 .
( 1 )把 向上平移6个单位后得到对应的 ,画出 ,并写出 的坐标;
( 2 )以原点 为对称中心,画出 关于原点对称的 ,并写出点 的坐标;
( 3 ) 与 是否为中心对称,如果是,请直接写出对称中心坐标:如果不是,请说明理由.
19. 如图,在平面直角坐标系中,矩形OABC的三个顶点A,O,C在坐标轴上,矩形的面积为12,对角线AC所在直线的解析式为y=kx-4k(k≠0). (1)、求A,C的坐标;(2)、若D为AC中点,过D的直线交y轴负半轴于E,交BC于F,且OE=1,求直线EF的解析式;(3)、在(2)的条件下,在坐标平面内是否存在一点G,使以C,D,F,G为顶点的四边形为平行四边形,若存在,请直接写出点G的坐标;若不存在,请说明理由.20. 在活动课上我们曾经探究过三角形内角和等于180°,四边形内角和等于360°,五边形内角和等于540°,…,请同学们仔细读题,看图,解决下面的问题:
(1)、求A,C的坐标;(2)、若D为AC中点,过D的直线交y轴负半轴于E,交BC于F,且OE=1,求直线EF的解析式;(3)、在(2)的条件下,在坐标平面内是否存在一点G,使以C,D,F,G为顶点的四边形为平行四边形,若存在,请直接写出点G的坐标;若不存在,请说明理由.20. 在活动课上我们曾经探究过三角形内角和等于180°,四边形内角和等于360°,五边形内角和等于540°,…,请同学们仔细读题,看图,解决下面的问题: (1)、如图①,△OAB、△OCD的顶点O重合,且∠A+∠B+∠C+∠D=180°,则∠AOB+∠COD=(直接写出结果).(2)、连接AD、BC,若AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线.
(1)、如图①,△OAB、△OCD的顶点O重合,且∠A+∠B+∠C+∠D=180°,则∠AOB+∠COD=(直接写出结果).(2)、连接AD、BC,若AO、BO、CO、DO分别是四边形ABCD的四个内角的平分线.①如图②,如果∠AOB=110°,求∠COD的度数.
②如图③,若∠AOD=∠BOC,AB与CD平行吗?请写出理由.
21. 如图,在平面直角坐标系中,一次函数 的图象经过点 ,与 轴交于点 ,与正比例函数 的图象相交于点 . (1)、求此一次函数的解析式;(2)、求出 的面积;(3)、点 在此坐标平面内,且知以 、 、 、 为顶点四边形是平行四边形,请直接写出符合条件的点 的坐标.22. △ABC在平面直角坐标系中如图所示,
(1)、求此一次函数的解析式;(2)、求出 的面积;(3)、点 在此坐标平面内,且知以 、 、 、 为顶点四边形是平行四边形,请直接写出符合条件的点 的坐标.22. △ABC在平面直角坐标系中如图所示, (1)、S△ABC= .(2)、x轴上是否存在点P,使得S△BCP=2S△ABC , 若不存在,说明理由;若存在,求出P点的坐标.(3)、请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.23. 已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P.
(1)、S△ABC= .(2)、x轴上是否存在点P,使得S△BCP=2S△ABC , 若不存在,说明理由;若存在,求出P点的坐标.(3)、请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.23. 已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P. (1)、点D、E分别在线段BA、BC上;
(1)、点D、E分别在线段BA、BC上;①若∠B=60°(如图1),且AD=BE,BD=CE,求∠APD的度数;
②若∠B=90°(如图2),且AD=BC,BD=CE,求∠APD的度数;
(2)、如图3,点D、E分别在线段AB、BC的延长线上,若∠B=90°,AD=BC,∠APD=45°,求证:BD=CE.24. 已知点O是△ABC内任意一点,连接OA并延长到点E,使得AE=OA,以OB,OC为邻边作平行四边形OBFC,连接OF,与BC交于点H,连接EF.(1)、问题发现:如图1,若△ABC为等边三角形,线段EF与BC的位置关系是 , 数量关系为; (2)、拓展探究:如图2,若△ABC为等腰直角三角形(BC为斜边),(1)中的两个结论是否成立?若成立,请给予证明;若不成立,请写出正确的结论再给予证明;
(2)、拓展探究:如图2,若△ABC为等腰直角三角形(BC为斜边),(1)中的两个结论是否成立?若成立,请给予证明;若不成立,请写出正确的结论再给予证明; (3)、解决问题:如图3,若△ABC是等腰三角形,AB=AC=5,BC=6,请你直接写出线段EF的长.
(3)、解决问题:如图3,若△ABC是等腰三角形,AB=AC=5,BC=6,请你直接写出线段EF的长.