初中数学浙教版八年级下册第四章 平行四边形 基础巩固训练
试卷更新日期:2021-04-17 类型:单元试卷
一、单选题
-
1. 下面列图案中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 从八边形的一个顶点引对角线,最多把它分割成三角形的个数为( )A、5 B、6 C、7 D、83. 一个多边形内角和是720º,则这个多边形的对角线条数为( )A、3 B、6 C、9 D、124. 下列说法中,正确的个数有:( )
2. 从八边形的一个顶点引对角线,最多把它分割成三角形的个数为( )A、5 B、6 C、7 D、83. 一个多边形内角和是720º,则这个多边形的对角线条数为( )A、3 B、6 C、9 D、124. 下列说法中,正确的个数有:( )①同旁内角互补;②直线外一点与直线上各点连接的所有线段中,垂线段最短;③从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;④平行线间的距离处处相等.
A、1个 B、2个 C、3个 D、4个5. 在平行四边形 中,若 ,则 的度数是( )A、50° B、60° C、70° D、80°6. 如图,在 中, 、 相交于点O, ,若 , ,则 的周长是( ) A、8 B、10 C、12 D、167. 能判定四边形ABCD是平行四边形的是( )A、AB∥CD,AB=CD B、AB=BC,AD=CD C、AC=BD,AB=CD D、AB∥CD,AD=CB8. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,E是BC边上的中点,若 ,则平行四边形ABCD的周长为( )
A、8 B、10 C、12 D、167. 能判定四边形ABCD是平行四边形的是( )A、AB∥CD,AB=CD B、AB=BC,AD=CD C、AC=BD,AB=CD D、AB∥CD,AD=CB8. 如图,在平行四边形ABCD中,对角线AC,BD交于点O,E是BC边上的中点,若 ,则平行四边形ABCD的周长为( ) A、9 B、16 C、18 D、209. 用反证法证明命题“在四边形中至少有一个内角不大于90°”时,首先应假设( )A、每个内角都小于90° B、每个内角都大于90° C、没有一个内角大于90° D、每个内角都等于90°10. 如图 是正五边形 的三个外角,若 则 =( )
A、9 B、16 C、18 D、209. 用反证法证明命题“在四边形中至少有一个内角不大于90°”时,首先应假设( )A、每个内角都小于90° B、每个内角都大于90° C、没有一个内角大于90° D、每个内角都等于90°10. 如图 是正五边形 的三个外角,若 则 =( )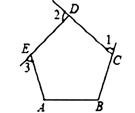 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若一个多边形的内角和与外角和之和是1800°,则此多边形是边形.12. 如图,直线AE∥BD,点C在BD上,若AE=4,BD=8,△ABD的面积为16,则 的面积为.
 13. 在①平行四边形;②矩形;③菱形;④正方形;⑤等腰梯形这五种图形中,既是轴对称图形又是中心对称图形的是(只填序号).14. 如图,在平行四边形 中, 两点均在对角线 上.要使四边形 为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是(写出一个即可).
13. 在①平行四边形;②矩形;③菱形;④正方形;⑤等腰梯形这五种图形中,既是轴对称图形又是中心对称图形的是(只填序号).14. 如图,在平行四边形 中, 两点均在对角线 上.要使四边形 为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是(写出一个即可).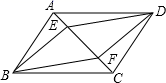 15. 如图,AD、BE是△ABC的两条中线,△EDC的面积是2,则△ABD的面积是 .
15. 如图,AD、BE是△ABC的两条中线,△EDC的面积是2,则△ABD的面积是 . 16. 各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式 (a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积 .
16. 各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式 (a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积 .
三、解答题
-
17. 一个多边形除了一个内角a外,其余内角的和为2680°,求这个多边形的边数和这个内角a的度数.18. 如图,在 中,∠ABC的平分线BE交AD于点E,测得∠AEB=27°,求∠D的度数.
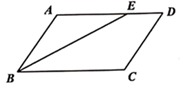 19. 的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证: ,且 .
19. 的中线BD,CE相交于O,F,G分别是BO,CO的中点,求证: ,且 . 20. 在不等边△ABC中,A是最小角,求证:A<60°.21. 如图是一种儿童的游乐设施—儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.
20. 在不等边△ABC中,A是最小角,求证:A<60°.21. 如图是一种儿童的游乐设施—儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由. 22. 如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,DE,BF与对角线AC分别交于点M,N,连接MF,NE.
22. 如图,在平行四边形ABCD中,E,F分别是AB,CD的中点,DE,BF与对角线AC分别交于点M,N,连接MF,NE. (1)、求证:DE∥BF(2)、判断四边形MENF是何特殊的四边形?并对结论给予证明;23. 如图,由4个全等的正方形组成L形图案,请按下列要求画图:
(1)、求证:DE∥BF(2)、判断四边形MENF是何特殊的四边形?并对结论给予证明;23. 如图,由4个全等的正方形组成L形图案,请按下列要求画图: (1)、在图①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);(2)、在图②中添加1个正方形,使它成中心对称图形(不能是轴对称图形);(3)、在图③中改变1个正方形的位置,从而得到一个新图形,使它既成中心对称图形,又成轴对称图形.24. 如图,平行四边形ABCO位于直角坐标系中,O为坐标原点,点 ,点 交y轴于点 动点E从点D出发,沿DB方向以每秒1个单位长度的速度终点B运动,同时动点F从点A出发,沿射线OA的方向以每秒2个单位长度的速度运动,当点E运动到点B时,点F随之停止运动,运动时间为 秒 .
(1)、在图①中添加1个正方形,使它成轴对称图形(不能是中心对称图形);(2)、在图②中添加1个正方形,使它成中心对称图形(不能是轴对称图形);(3)、在图③中改变1个正方形的位置,从而得到一个新图形,使它既成中心对称图形,又成轴对称图形.24. 如图,平行四边形ABCO位于直角坐标系中,O为坐标原点,点 ,点 交y轴于点 动点E从点D出发,沿DB方向以每秒1个单位长度的速度终点B运动,同时动点F从点A出发,沿射线OA的方向以每秒2个单位长度的速度运动,当点E运动到点B时,点F随之停止运动,运动时间为 秒 .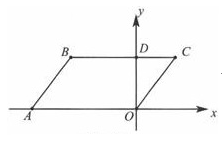 (1)、用t的代数式表示: ,(2)、若以A,B,E,F为顶点的四边形是平行四边形时,求t的值.(3)、当 恰好是等腰三角形时,求t的值.
(1)、用t的代数式表示: ,(2)、若以A,B,E,F为顶点的四边形是平行四边形时,求t的值.(3)、当 恰好是等腰三角形时,求t的值.