初中数学浙教版八年级下册4.5 三角形的中位线 同步练习
试卷更新日期：2021-04-17 类型：同步测试
一、单选题
-
1. 如图，D、E分别是△ABC的边AB、AC的中点，若BC＝6，则DE＝（ ）
A、2 B、3 C、4 D、52. 如图，要测定被池塘隔开的A，B两点的距离，可以在AB外选一点C，连接AC，BC，并分别找出它们的中点D，E，连接ED.现测得AC=42m，BC=64m，DE=26m，则AB等于（ ）
A、42m B、52m C、56m D、64m3. 如图，在△ABC中，点D、E、F分别是BC、AB、AC的中点，如果△ABC的周长为20，那么△DEF的周长是（ ）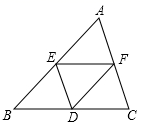
A、20 B、15 C、10 D、54. 如图，顺次连接四边形ABCD各边中点得四边形EFGH，要使四边形EFGH为矩形，则应添加的条件是（ ）
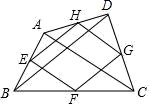A、AB//CD B、AC⊥BD C、AC=BD D、AD=BC5. Rt△ABC两直角边的长分别为6cm和8cm，则连接这两条直角边中点的线段长为（ ）A、10cm B、3cm C、4cm D、5cm6. 如图，在平行四边形ABCD中，已知 分别是线段OD，OA的中点，则EF的长为（ ）
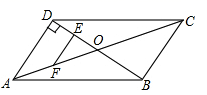A、3 B、4 C、5 D、87. 如图， 对角线 相交于O点，E是 的中点，连接 ，若 则 的周长是（ ）
A、 B、 C、 D、8. 若三角形的各边长分别是8，10和16，则以各边中点为顶点的三角形的周长为（ ）A、34 B、30 C、29 D、179. 如图，在四边形ABCD中，P是对角线BD的中点，点E、F分别是AB、CD的中点，AD＝BC，∠EPF＝140°，则∠EFP的度数是（ ）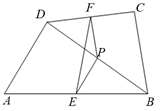
A、50° B、40° C、30° D、20°10. 如图，E ， F是四边形ABCD两边AB ， CD的中点，G ， H是对角线AC ， BD的中点，若EH=6，则以下结论错误的是（ ）
A、 B、 C、 D、二、填空题
-
11. 如图是屋架设计图的一部分，点D是斜梁AB的中点，立柱BC、DE垂直于横梁AC，AB＝7.4m，∠A＝30°，则DE长为.
12. 已知在△ABC中，AB=BC=10，AC=8，AF⊥BC于点F，BE⊥AC于点E，取AB的中点D，则△DEF的周长为.
13. 如图，D是 内一点， ， 分别是 的中点，若 ，则四边形 的周长是.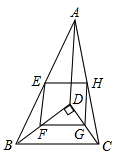
14. 在Rt△ABC中，∠C=90°，AC=3，BC=4，点N是BC边上一点，点M为AB边上的动点，点D、E分别为CN、MN的中点，则DE长度的取值范围是.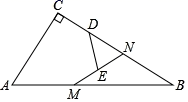
三、解答题
-
15. 如图已知Rt△ABC中，∠ACB=90°，∠B=15°，边AB的垂直平分线交边BC 于点E，垂足为点D，取线段BE的中点F，联结 DF，求证：AC=DF。
16. 如图，在 中， ，点D在 的延长线上，连接 ，E为 的中点.请用尺规作图法在 边上求作一点F，使得 为 的中位线.（保留作图痕迹，不写作法）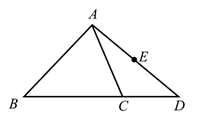
17. 如图，▱ABCD的对角线AC、BD相交于点O，且E、F、G、H分别是AO、BO、CO、DO的中点.
(1)、求证：四边形EFGH是平行四边形；(2)、若AC+BD=36，AB=10，求△OEF的周长.18. 如图所示，在四边形ABCD中，E是BC的中点，F是线段DE上一点（不与点D重合），AB∥DE，AE∥DC.
(1)、如图1，当点F与E重合时，求证：四边形AFCD是平行四边形；(2)、如图2，当点F不与E重合时，（1）中的结论还成立吗？请说明理由.(3)、如图3，当∠BCD=90°，且CD=CE，F恰好运动到DE的中点时，直接写出AB与DC的数量关系.