初中数学浙教版八年级下册4.2.2平行线间的线段 同步练习
试卷更新日期：2021-04-17 类型：同步测试
一、单选题
-
1. 如图所示， ∥ ，则平行线 与 间的距离是（ ）
A、线段AB的长度 B、线段BC的长度 C、线段CD的长度 D、线段DE的长度2. 平行线之间的距离是指（ ）A、从一条直线上一点到另一条直线的垂线段； B、从一条直线上一点到另一条直线的垂线段长度； C、从一条直线上一点到另一条直线的垂线的长度； D、从一条直线上一点到另一条直线上的一点间线段的长度.3. 如图，直线l1∥l2 ， 线段AB的端点A，B分别在直线11和12上，AB＝6.点C在直线12上，∠ABC＝30°，则这两条直线的距离是（ ）
A、3 B、6 C、2 D、34. 如图，直线 ，点P是直线 上一个动点，当点P的位置发生变化时，三角形 的面积（ ）
A、向左移动变小 B、向右移动变小 C、始终不变 D、无法确定5. 把线段 沿水平方向平移 ，平移后为线段 ，则线段 与线段 之间的距离是（ ）.A、等于 B、小于 C、小于或等于 D、大于或等于6. 如图，一绿地的两边AD，BC平行，绿地中间开辟两条道路，而每条道路的宽处处相等，且EF=GH=PQ=MN，则两条道路的占地面积情况是（ ）
A、不相等 B、四边形GHNM面积要大 C、四边形EFQP的面积大 D、相等7. 如图，AB∥DC，ED∥BC，AE∥BD，那么图中和△ABD面积相等的三角形（不包括△ABD）有（ ）
A、1个 B、2个 C、3个 D、4个8. 直线a上有一点A，直线b上有一点B，且a∥b．点P在直线a，b之间，若PA=3，PB=4，则直线a、b之间的距离（ ）A、等于7 B、小于7 C、不小于7 D、不大于79. 如图，四边形ABCD中，AD∥BC，AC与BD相交于点O，若S△ABD=10cm2 ， S△ACD为（ ）
A、10 B、9 C、8 D、710. 如图 ，若 表示三角形 的面积， 表示三角形 的面积，则下列结论正确的是（ ）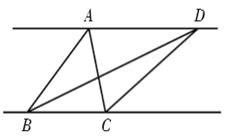
A、 B、 C、 D、二、填空题
-
11. 两条平行线间的所有线段都相等．12. 如图所示， ，表示直线a与b之间距离的是线段的长度．
13. 如图，已知 ， ， ，且 ， 垂足分别为E，F．则AD与BC间的距离是 ．
14. 在□ABCD 中，∠A=150°，AB=8cm，BC=10cm，若点 P 是□ABCD 上 AD 上任意一点，那么△PBC 的面积是
三、综合题
-
15. 已知直线a，b，a平行于b，过直线a上任意两点A，B分别向直线b作垂线，交直线b于点C，D．
(1)、线段AC，BD所在的直线有怎样的位置关系？(2)、比较线段AC，BD的长短．16. 有这样的一个定理：夹在两条平行线间的平行线段相等．下面经历探索与应用的过程．
(1)、探索：已知：如图1，AD∥BC，AB∥CD．求证：AB=CD．
应用此定理进行证明求解．
(2)、应用一、已知：如图2，AD∥BC，AD＜BC，AB=CD．求证：∠B=∠C；(3)、应用二、已知：如图3，AD∥BC，AC⊥BD，AC=4，BD=3．求：AD与BC两条线段的和．17. 如图，在△ABC中，BC=6cm．射线AG∥BC，点E从点A出发沿射线AG以2cm/s的速度运动，当点E先出发1s后，点F也从点B出发沿射线BC以 cm/s的速度运动，分别连结AF，CE．设点F运动时间为t（s），其中t＞0．
(1)、当t为何值时，∠BAF＜∠BAC；(2)、当t为何值时，AE=CF；(3)、当t为何值时，S△ABF+S△ACE＜S△ABC ．