初中数学浙教版八年级下册4.1 多边形 同步练习

试卷更新日期：2021-04-17 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 一个多边形有5条边，则它的内角和是（ ）
    A、540° B、720° C、900° D、1080°

    查看试题解析

  • 2. 如图，已知 △ABC 中， ∠A=70° ，则 ∠1+∠2= （   ）.

    A、290° B、250° C、150° D、145°

    查看试题解析

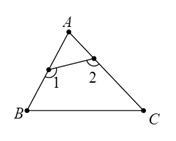  • 3. 一个n边形的每一个外角都是72°，则n等于（　　）
    A、3 B、4 C、5 D、6

    查看试题解析

  • 4. 过多边形的一个顶点能引出7条对角线，则这个多边形是（   ）边形
    A、七 B、八 C、九 D、十

    查看试题解析

  • 5. 若一个正多边形的内角和等于其外角和的3倍，则这个正多边形是（   ）
    A、5边形 B、6边形 C、7边形 D、8边形

    查看试题解析

  • 6. 一个多边形每一个外角都等于 36° ，则这个多边形的边数为（   ）
    A、12 B、10 C、8 D、6

    查看试题解析

  • 7. 如图，在五边形ABCDE中，AB∥CD ， ∠A＝135°，∠C＝60°，∠D＝150°，则∠E的大小为（   ）

    A、60° B、65° C、70° D、75°

    查看试题解析

  • 8. 一个多边形截去一个角后，形成的另一个多边形的内角和是 1620° ，则原来多边形的边数是（    ）
    A、11 B、12 C、11或12 D、10或11或12

    查看试题解析

  • 9. 将一个多边形纸片剪去一个内角后得到一个内角和是外角和4倍的新多边形，则原多边形的边数为（    ）
    A、9 B、10 C、11 D、以上均有可能

    查看试题解析

  • 10. n边形所有对角线的条数有（   ）
    A、n(n−1)2 条 B、n(n−2)2 条 C、n(n−3)2 条 D、n(n−4)2 条

    查看试题解析

二、填空题

  • 11. 从n边形的一个顶点可以引出2020条对角线，则n的值为

    查看试题解析

  • 12. 多边形每一个内角都等于144°，则从此多边形一个顶点出发的对角线有条.

    查看试题解析

  • 13. 从n边形的一个顶点出发，连接其余各顶点，可以将这个n边形分割成17个三角形，则n＝.

    查看试题解析

  • 14. 对于一个四边形的四个内角，下面四个结论中，①可以四个角都是锐角；②至少有两个角是锐角；③至少有一个角是钝角；④最多有三个角是钝角；所有正确结论的序号是 ．

    查看试题解析

三、解答题

  • 15. 已知两个多边形的所有内角的和为1800°，且两个多边形的边数之比为2：5，求这两个多边形的边数.

    查看试题解析

  • 16. 如图是一个凹多边形， ∠A=90∘ ， ∠C=106∘ ， ∠D=119∘ ， ∠E=100∘ ；求 ∠1+∠2 的值．

    查看试题解析

  • 17. 已知 n 边形的内角和 θ=(n−2)×180° .
    (1)、当 θ=900° 时，求出边数 n ；
    (2)、小明说， θ 能取 800° ，这种说法对吗？若对，求出边数 n ；若不对，说明理由.

    查看试题解析

  • 18. 如图是一个多边形，你能否用一直线去截这个多边形，使得到的新多边形分别满足下列条件： ( 画出图形，把截去的部分打上阴影 )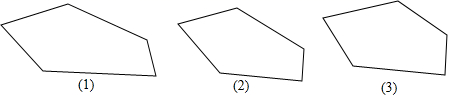

    (1)、①新多边形内角和比原多边形的内角和增加了 180∘ ．

    ②新多边形的内角和与原多边形的内角和相等．

    ③新多边形的内角和比原多边形的内角和减少了 180∘ ．

    (2)、将多边形只截去一个角，截后形成的多边形的内角和为 2520∘ ，求原多边形的边数．

    查看试题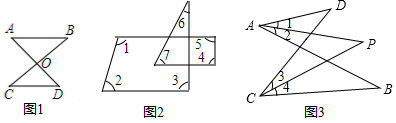解析

  • 19. 如图

    (1)、如图1我们称之为“8字形”，请直接写出∠A，∠B，∠C，∠D之间的数量关系：；
    (2)、如图2，∠1+∠2+∠3+∠4+∠5+∠6+∠7＝度；
    (3)、如图3所示，已知∠1＝∠2，∠3＝∠4，猜想∠B，∠P，∠D之间的数量关系，并证明．

    查看试题解析