初中数学湘教版八年级下册4.1.1变量与函数 同步练习
试卷更新日期:2021-04-17 类型:同步测试
一、单选题
-
1. 下列图象中,表示y是x的函数的有 ( )
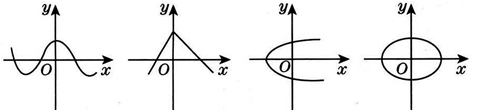 A、1个 B、2个 C、3个 D、4个2. 函数y= 中,自变量x的取值范围是( )A、x=-2 B、x=1 C、x≠-2 D、x≠13. 下列说法正确的是( )A、常量是指永远不变的量 B、具体的数一定是常量 C、字母一定表示变量 D、球的体积公式V= πr³,变量是π,r4. 为了建设社会主义新农村,我市积极推进“行政村通畅工程”.张村和王村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间的道路改造.下面能反映该工程尚未改造的道路里程y(公里)与时间x(天)的函数关系的大致图象是( )A、
A、1个 B、2个 C、3个 D、4个2. 函数y= 中,自变量x的取值范围是( )A、x=-2 B、x=1 C、x≠-2 D、x≠13. 下列说法正确的是( )A、常量是指永远不变的量 B、具体的数一定是常量 C、字母一定表示变量 D、球的体积公式V= πr³,变量是π,r4. 为了建设社会主义新农村,我市积极推进“行政村通畅工程”.张村和王村之间的道路需要进行改造,施工队在工作了一段时间后,因暴雨被迫停工几天,不过施工队随后加快了施工进度,按时完成了两村之间的道路改造.下面能反映该工程尚未改造的道路里程y(公里)与时间x(天)的函数关系的大致图象是( )A、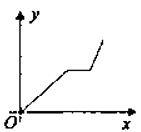 B、
B、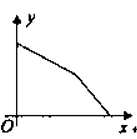 C、
C、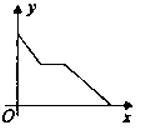 D、
D、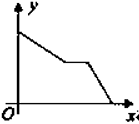 5. 一根弹簧原长12cm,它所挂的重量不超过10kg,并且挂重1kg就伸长1.5cm,写出挂重后弹簧长度y(cm)与挂重x(kg)之间的函数关系式是( )A、y=1.5(x+12)(0≤x≤10) B、y=1.5x+12(0≤x≤10) C、y=1.5x+12(x≥0) D、y=1.5(x﹣12)(0≤x≤10)6. 已知函数y= ,则当函数值y=8时,自变量x的值是( )A、﹣2或4 B、4 C、﹣2 D、±2或±47. 设半径为r的圆的面积为S,则S=πr2 , 下列说法错误的是( )
5. 一根弹簧原长12cm,它所挂的重量不超过10kg,并且挂重1kg就伸长1.5cm,写出挂重后弹簧长度y(cm)与挂重x(kg)之间的函数关系式是( )A、y=1.5(x+12)(0≤x≤10) B、y=1.5x+12(0≤x≤10) C、y=1.5x+12(x≥0) D、y=1.5(x﹣12)(0≤x≤10)6. 已知函数y= ,则当函数值y=8时,自变量x的值是( )A、﹣2或4 B、4 C、﹣2 D、±2或±47. 设半径为r的圆的面积为S,则S=πr2 , 下列说法错误的是( )A.
A、变量是S和r B、常量是π和2 C、用S表示r为 D、常量是π
8. 下列表达形式中,能表示y是x的函数的是( )A、|y|=x B、y=± C、
D、常量是π
8. 下列表达形式中,能表示y是x的函数的是( )A、|y|=x B、y=± C、 D、
D、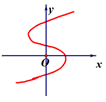 9. 汽车由A市驶往相距120km的B市,它的平均速度是30km/h,则汽车距B市的路程s(km)与行驶时间t(h)的函数关系式及自变量的取值范围是( )A、 B、 C、 D、10.
9. 汽车由A市驶往相距120km的B市,它的平均速度是30km/h,则汽车距B市的路程s(km)与行驶时间t(h)的函数关系式及自变量的取值范围是( )A、 B、 C、 D、10.如图,在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG,动点P从点A出发,沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止(不含点A和点B),则△ABP的面积S随着时间t变化的函数图象大致是( )
 A、
A、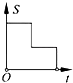 B、
B、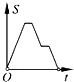 C、
C、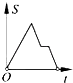 D、
D、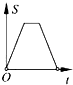
二、填空题
-
11. 如果点A(1,m)在直线 上,那么m= .12. 圆的面积公式 中,变量是 ,常量是.13. 一个正方形的边长为5cm,它的边长减少xcm后得到的新正方形的周长为ycm,则y与x的关系式是 , 自变量的取值范围是 .14. 下列变量间的关系是函数关系的有(填序号)
①正方形的周长与边长; ②圆的面积与半径;
③等腰三角形的底边长与面积; ④商场中某种商品的单价为a元,销售总额与销售数量
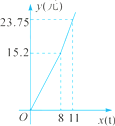
15. 一慢车和一快车沿相同路线从A地到B地,所行的路程与时间图象如图,则慢车比快车早出发小时,快车追上慢车行驶了千米,快车比慢车早小时到达B地.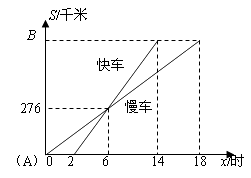
三、解答题
-
16. 我国是一个严重缺水的国家,我们都应该倍加珍惜水资源,节约用水.据测试,拧不紧的水龙头每秒会滴下2滴水,每滴水约0.5毫升.小燕子同学在洗手时,没有拧紧水龙头,当小燕子离开x(时)后水龙头滴了y(毫升)水.在这段文字中涉及的量中,哪些是常量,哪些是变量?17. 已知函数f(x)= ,求函数的定义域及f(4).
四、综合题
-
18. 一个梯形,它的下底比上底长2cm,它的高为3cm,设它的上底长为xcm,它的面积为ycm2.(1)、写出y与x之间的关系式,并指出哪个变量是自变量,哪个变量是因变量.(2)、当x由5变7时,y如何变化?(3)、用表格表示当x从3变到10时(每次增加1),y的相应值.(4)、当x每增加1时,y如何变化?说明你的理由.