初中数学华师大版七年级下学期期中考试复习专题：03 三元一次方程组-在线组卷题库

1. 如图所示，两个天平都平衡，则三个苹果的重量等于多少个香蕉的重量？答（）个.

A、2 B、3 C、4 D、5

查看试题解析
2. 我国古代数学家张丘建在《张丘建算经）里，提出了“百钱买百鸡”这个有名的数学问题.用100个钱买100只鸡，公鸡每只五个钱，母鸡每只三个钱，小鸡每个钱三只.问公鸡，小鸡各买了多少只？在这个问题中，小鸡的只数不可能是（）

A、87 B、84 C、81 D、78

查看试题解析
3. 已知 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ 是二元一次方程组 ${\begin{array}{l} a x + c y = 1 \\ c x - b y = 2 \end{array}$ 的解，则a，b间的关系为（）

A、 $a + b = 3$ B、 $a - b = - 1$ C、 $a + b = 0$ D、 $a - b = - 3$

查看试题解析
4. 某商场推出A、B、C三种特价玩具，若购买A种2件、B种1件、C种3件，共需24元；若购买A种3件、B种4件、C种2件，共需36元．那么小明购买A种1件、B种1件、C种1件，共需付款（）

A、11元 B、12元 C、13元 D、不能确定

查看试题解析
5. 已知方程组 ${\begin{array}{l} x - y = 5 \\ 4 x - 3 y + k = 0 \end{array}$ 的解也是方程3x－2y=0的解，则k的值是（）

A、k=－5 B、k=5 C、k=－10 D、k=10

查看试题解析

6. 设 ${\begin{array}{l} 2 x + y + 3 z = 23 \\ x + 4 y + 5 z = 36 \end{array}$ ，则3x-2y+z= ．

查看试题解析
7. 在刚刚结束的万州二中秋季运动会中，有一个趣味项目，5分钟内运送三大筐数量相同的兵乓球，甲每次从第一个大筐中取出9个球；乙每次从第二个大筐中取出7个球；丙则是每次从第三个大筐中取出5个球.比赛激烈最终三人都记不清各自取了多少次球了，最后裁判清点发现第一个筐中剩下7个球，第二个筐剩下4个球，第三个筐剩下2个球，那么根据上述情况可以推知每个筐中至少有个兵乓球.

查看试题解析
8. 为确保信息安全，在传输时往往需加密，发送方发出一组密码a，b，c时，则接收方对应收到的密码为A，B，C，双方约定：A＝2a－b，B＝2b，C＝b＋c，例如发出的密码是1，2，3，则收到的密码是0，4，5.若接收方收到的密码是2，8，11时，则发送方发出的密码是

查看试题解析

9. 解方程组： ${\begin{matrix} 3 x + 4 z = 7 ① \\ \begin{array}{l} 2 x + 3 y + z = 9 ② \\ 5 x - 9 y + 7 z = 8 ③ \end{array} \end{matrix}$

查看试题解析
10.

(1)、解不等式组 ${\begin{array}{l} x - 3 (x - 2) \geq 4 \\ \frac{2 x - 1}{5} > \frac{x + 1}{2} \end{array}$

(2)、在等式 $y = a x^{2} + b x + c$ 中，当 $x = - 1$ 时， $y = 0$ ；当 $x = 2$ 时， $y = 3$ ；当 $x = 5$ 时， $y = 60$ ，求a，b，c的值.

查看试题解析

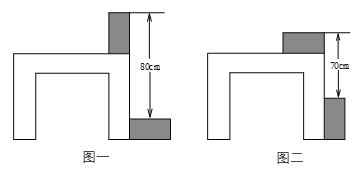
11. 一个三位数，如果把它的个位数字与百位数字交换位置，那么所得的新数比原数小99，且各位数字之和为14，十位数字是个位数字与百位数字之和．求这个三位数．

查看试题解析
12. 利用两块完全相同的长方形木块测量一张桌子的高度，首先将木块按图一方式放置，再交换两木块的位置，按图二方式放置，测量数据如图，求桌子的高度.

查看试题解析
13. 在等式y＝ax²+bx+c中，当x＝﹣1时，y＝3；当x＝0时，y＝1，当x＝1时，y＝1，求这个等式中a、b、c的值.

查看试题解析

14. 阅读感悟：
有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的代数式的值，如以下问题：

已知实数x、y满足 $3 x - y = 5$ ①， $2 x + 3 y = 7$ ②，求 $x - 4 y$ 和 $7 x + 5 y$ 的值.

本题常规思路是将①②两式联立组成方程组，解得x、y的值再代入欲求值的代数式得到答案，常规思路运算量比较大.其实，仔细观察两个方程未知数的系数之间的关系，本题还可以通过适当变形整体求得代数式的值，如由① $-$ ②可得 $x - 4 y = - 2$ ，由① $+$ ② $\times 2$ 可得 $7 x + 5 y = 19$ .这样的解题思想就是通常所说的“整体思想”.

解决问题：

(1)、已知二元一次方程组 ${\begin{array}{l} 2 x + y = 7 \\ x + 2 y = 8 \end{array}$ ，则 $x - y =$ ， $x + y =$ ；

(2)、某班级组织活动购买小奖品，买20支铅笔、3块橡皮、2本日记本共需32元，买39支铅笔、5块橡皮、3本日记本共需58元，则购买5支铅笔、5块橡皮、5本日记本共需多少元？

(3)、对于实数x、y，定义新运算： $x * y = a x + b y + c$ ，其中a、b、c是常数，等式右边是通常的加法和乘法运算.已知 $3 * 5 = 15$ ， $4 * 7 = 28$ ，那么 $1 * 1 =$ .

查看试题解析
15. 某商场计划用56000元从厂家购进60台新型电子产品，已知该厂家生产甲乙、丙三种不同型号的电子产品，设甲、乙型设备应各买入x，y台，其中每台的价格、销售获利如下表：

甲型

乙型

丙型

价格(元/台)

1000

800

500

销售获利(元/台)

260

190

120

(1)、购买丙型设备台(用含x，y的代数式表示)；

(2)、若商场同时购进三种不同型号的电子产品(每种型号至少有一台)，恰好用了56000元，则商场有哪几种购进方案？

(3)、在第(2)题的基础上，为了使销售时获利最多，应选择哪种购进方案？此时获利为多少？

查看试题解析

初中数学华师大版七年级下学期期中考试复习专题：03 三元一次方程组

一、单选题

二、填空题

三、计算题

四、解答题

五、综合题

	甲型	乙型	丙型
价格(元/台)	1000	800	500
销售获利(元/台)	260	190	120