湖北省武汉市江汉区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2021-04-16 类型:期末考试
一、选择题
-
1. 二次根式 中x的取值范围是( )A、 B、 C、 D、2. 下列各曲线中,表示y是x的函数是( )A、
 B、
B、 C、
C、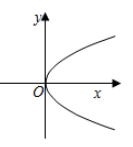 D、
D、 3. 下列运算正确的是A、 B、 C、 D、4. 如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )
3. 下列运算正确的是A、 B、 C、 D、4. 如图,在△ABC中,点D、E、F分别是BC、AB、AC的中点,如果△ABC的周长为20,那么△DEF的周长是( )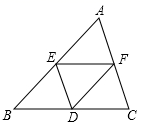 A、20 B、15 C、10 D、55. 甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2s,方差如下表:
A、20 B、15 C、10 D、55. 甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2s,方差如下表:选手
甲
乙
丙
丁
方差(s2)
0.020
0.019
0.021
0.022
则这四人中发挥最稳定的是( )
A、甲 B、乙 C、丙 D、丁6. 一次函数y=﹣3x+5的图象不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 已知四边形 是平行四边形,下列结论中不正确的是( )A、当 时,它是菱形 B、当 时,它是菱形 C、当 时,它是矩形 D、当 时,它是正方形8. 的三边长分别为 ,下列条件:① ;② ;③ ;④ 其中能判断 是直角三角形的个数有( )A、 个 B、 个 C、 个 D、 个9. 已知 是一次函数 的图象上三点,则 的大小关系为( )A、 B、 C、 D、10. 如图所示,购买一种苹果,所付款金额y(单元:元)与购买量x(单位:千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果,比分五次购买,每次购买1千克这种苹果可节省( ) A、10元 B、6元 C、5元 D、4元
A、10元 B、6元 C、5元 D、4元二、填空题
-
11. 计算: .12. 直线 与直线 平行,则 .13. 统计学校排球队队员的年龄,发现有12岁、13岁、14岁、15岁等四种年龄,统计结果如下表,则根据表中信息可以判断该排球队队员的平均年龄是岁.
年龄/岁
12
13
14
15
人数/个
2
4
6
8
14. 如图,在正方形 的外侧,作等边 ,则 的度数是 . 15. 如图,直线 与直线 交于点 ,则不等式 的解集是.
15. 如图,直线 与直线 交于点 ,则不等式 的解集是.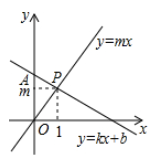 16. 如图,正方形OMNP的定点与正方形ABCD的对角线交点O重合,正方形ABCD和正方形OMNP的边长都是2cm,则图中重叠部分的面积是 .
16. 如图,正方形OMNP的定点与正方形ABCD的对角线交点O重合,正方形ABCD和正方形OMNP的边长都是2cm,则图中重叠部分的面积是 . 17. 已知 ,则 .18. 甲、乙两车从 城出发匀速行驶至 城在个行驶过程中甲乙两车离开 城的距离 (单位:千米)与甲车行驶的时间 (单位:小时)之间的函数关系如图所示.则下列结论: ① 两城相距 千米;②乙车比甲车晚出发 小时,却早到 小时;③乙车出发后 小时追上甲车;④在乙车行驶过程中.当甲、乙两车相距 千米时, 或 ,其中正确的结论是.
17. 已知 ,则 .18. 甲、乙两车从 城出发匀速行驶至 城在个行驶过程中甲乙两车离开 城的距离 (单位:千米)与甲车行驶的时间 (单位:小时)之间的函数关系如图所示.则下列结论: ① 两城相距 千米;②乙车比甲车晚出发 小时,却早到 小时;③乙车出发后 小时追上甲车;④在乙车行驶过程中.当甲、乙两车相距 千米时, 或 ,其中正确的结论是.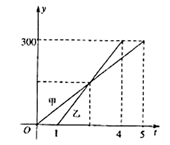 19. 在正方形 中,点 在边 上,点 在线段 上,且 则 度,四边形 的面积 .
19. 在正方形 中,点 在边 上,点 在线段 上,且 则 度,四边形 的面积 .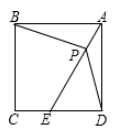 20. 如图,已知矩形 的边 将矩形的一部分沿 折叠,使 点与 点重合,点 的对应点为 ,则 的长是将 绕看点 顺时针旋转角度 得到 直线 分别与射线 ,射线 交于点 当 时, 的长是.
20. 如图,已知矩形 的边 将矩形的一部分沿 折叠,使 点与 点重合,点 的对应点为 ,则 的长是将 绕看点 顺时针旋转角度 得到 直线 分别与射线 ,射线 交于点 当 时, 的长是.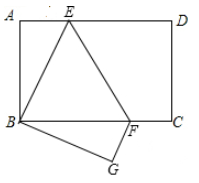
三、解答题
-
21. 计算下列各题:(1)、 ;(2)、 .22. 如图,矩形ABCD的对角线 相交于点 .
 (1)、判断四边形OCED的形状,并进行证明;(2)、若 ,求四边形OCED的面积.23. 如图, 城气象台测得台风中心在 城正西方向 的 处,以每小时 的速度向南偏东 的 方向移动,距台风中心 的范围内是受台风影响的区域.
(1)、判断四边形OCED的形状,并进行证明;(2)、若 ,求四边形OCED的面积.23. 如图, 城气象台测得台风中心在 城正西方向 的 处,以每小时 的速度向南偏东 的 方向移动,距台风中心 的范围内是受台风影响的区域. (1)、求 城与台风中心之间的最小距离;(2)、求 城受台风影响的时间有多长?24. 八年级全体同学参加了学校捐款活动,随机抽取了部分同学捐款的情况统计图如图所示
(1)、求 城与台风中心之间的最小距离;(2)、求 城受台风影响的时间有多长?24. 八年级全体同学参加了学校捐款活动,随机抽取了部分同学捐款的情况统计图如图所示 (1)、 本次共抽查学生人,并将条形统计图补充完整;(2)、 捐款金额的众数是 , 中位数是;(3)、在八年级600名学生中,捐款20元及以上的学生估计有人.25. 已知函数 ,
(1)、 本次共抽查学生人,并将条形统计图补充完整;(2)、 捐款金额的众数是 , 中位数是;(3)、在八年级600名学生中,捐款20元及以上的学生估计有人.25. 已知函数 ,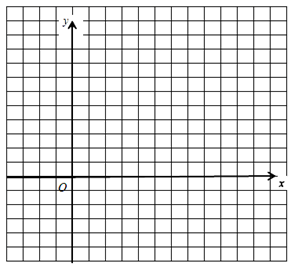 (1)、在平面直角坐标系中画出函数图象;(2)、函数图象与x轴交于点A,与y轴交于点B,已知 是图象上一个动点,若 的面积为6,求P点坐标;(3)、已知直线 与该函数图象有两个交点,求k的取值范围.26. 某体育用品商场采购员要到厂家批发购买篮球和排球共 个,篮球个数不少于排球个数,付款总额不得超过 元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购 个篮球.
(1)、在平面直角坐标系中画出函数图象;(2)、函数图象与x轴交于点A,与y轴交于点B,已知 是图象上一个动点,若 的面积为6,求P点坐标;(3)、已知直线 与该函数图象有两个交点,求k的取值范围.26. 某体育用品商场采购员要到厂家批发购买篮球和排球共 个,篮球个数不少于排球个数,付款总额不得超过 元,已知两种球厂的批发价和商场的零售价如下表. 设该商场采购 个篮球.品名
厂家批发价/元/个
商场零售价/元/个
篮球
排球
(1)、求该商场采购费用 (单位:元)与 (单位:个)的函数关系式,并写出自变最 的取值范围:(2)、该商场把这 个球全都以零售价售出,求商场能获得的最大利润;(3)、受原材料和工艺调整等因素影响,采购员实际采购时,低球的批发价上调了 元/个,同时排球批发价下调了 元/个.该体有用品商场决定不调整商场零售价,发现将 个球全部卖出获得的最低利润是 元,求 的值.27. 如图,正方形 ,点 在边 上, 为等腰直角三角形. (1)、如图1,当 ,求证 ;(2)、如图2,当 ,取 的中点 ,连接 ,求证:
(1)、如图1,当 ,求证 ;(2)、如图2,当 ,取 的中点 ,连接 ,求证: