湖北省武汉市黄陂区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2021-04-16 类型:期末考试
一、选择题
-
1. 计算 的结果是( )A、-3 B、3 C、6 D、92. 以下列各组数为边长,能构成直角三角形的是( )A、 B、2,2,3 C、 D、4,5,63. 将直线 沿y轴向下平移1个单位长度后得到的直线解析式为( )A、 B、 C、 D、4. 在某校举行的“我的中国梦”演讲比赛中,有5名学生参加决赛,他们决赛的最终成绩各不相同,其中的一名学生要想知道自己能否进入前3名,不仅要了解自己的成绩,还要了解这5名学生成绩的( )A、众数 B、方差 C、中位数 D、平均数5. 电视塔越高,从塔顶发射出的电磁波传播得越远,从而能收看到电视节目的区域就越广.电视塔高h(单位:km)与电视节目信号的传播半径r(单位:km)之间存在近似关系 ,其中R是地球半径.如果两个电视塔的高分别是 , ,那么它们的传播半径之比是 ,则式子 化简为( )A、 B、 C、 D、6. 如图是自动测温仪记录的图象,它反映了武汉的冬季某天气温 随时间 的变化而变化的情况,下列说法错误的是( )
 A、这一天凌晨4时气温最低 B、这一天14时气温最高 C、从4时至14时气温呈上升状态(即气温随时间增长而上升) D、这一天气温呈先上升后下降的趋势7. 如图,用一根绳子检查一个书架的侧边是否和上、下底都垂直,只需要用绳子分别测量比较书架的两条对角线 就可以判断,其数学依据是( )
A、这一天凌晨4时气温最低 B、这一天14时气温最高 C、从4时至14时气温呈上升状态(即气温随时间增长而上升) D、这一天气温呈先上升后下降的趋势7. 如图,用一根绳子检查一个书架的侧边是否和上、下底都垂直,只需要用绳子分别测量比较书架的两条对角线 就可以判断,其数学依据是( ) A、三个角都是直角的四边形是矩形 B、对角线互相平分的四边形是平行四边形 C、对角线相等的平行四边形是矩形 D、对角线互相垂直平分的四边形是菱形8. 甲、乙、丙三人进行射击测试,每人10次射击的平均成绩恰好都是9.2环,方差分别是 , . ,在本次射击测试中,成绩最稳定的是( )A、甲 B、乙 C、丙 D、无法确定9. 如图,在矩形ABCD中, , ,点M,N同时从点A出发,分别沿 及 方向匀速运动,速度均为每秒1个单位长度,当一个点到达终点时另一个点也停止运动,连接MN,设运动时间为t秒,MN的长为d,则下列图象能大致反映d与t的函数关系的是( )
A、三个角都是直角的四边形是矩形 B、对角线互相平分的四边形是平行四边形 C、对角线相等的平行四边形是矩形 D、对角线互相垂直平分的四边形是菱形8. 甲、乙、丙三人进行射击测试,每人10次射击的平均成绩恰好都是9.2环,方差分别是 , . ,在本次射击测试中,成绩最稳定的是( )A、甲 B、乙 C、丙 D、无法确定9. 如图,在矩形ABCD中, , ,点M,N同时从点A出发,分别沿 及 方向匀速运动,速度均为每秒1个单位长度,当一个点到达终点时另一个点也停止运动,连接MN,设运动时间为t秒,MN的长为d,则下列图象能大致反映d与t的函数关系的是( )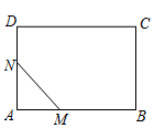 A、
A、 B、
B、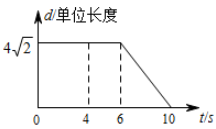 C、
C、 D、
D、 10. 如图,正方形ABCD的边长为2,点E为AD的中点,连接BE,将 沿BE折叠,点A的对应点为F.连接CF,则CF的长为( )
10. 如图,正方形ABCD的边长为2,点E为AD的中点,连接BE,将 沿BE折叠,点A的对应点为F.连接CF,则CF的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算 的结果是 .12. 在一列数2,3,3,5,7中,他们的平均数为.13. 某地出租车行驶里程 ( )与所需费用 (元)的关系如图.若某乘客一次乘坐出租车里程12 ,则该乘客需支付车费元.
 14. 如图,在菱形ABCD中,点E为AB上一点, ,连接EC.若 ,则 的度数为 .
14. 如图,在菱形ABCD中,点E为AB上一点, ,连接EC.若 ,则 的度数为 . 15. 已知一次函数 ( )经过点 ,则不等式 的解集为.16. 如图,矩形ABCD全等于矩形BEFG,点C在BG上.连接DF,点H为DF的中点.若 , ,则CH的长为.
15. 已知一次函数 ( )经过点 ,则不等式 的解集为.16. 如图,矩形ABCD全等于矩形BEFG,点C在BG上.连接DF,点H为DF的中点.若 , ,则CH的长为.
三、解答题
-
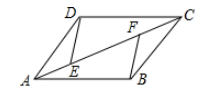
17. 计算:(1)、(2)、18. 如图,点E,F分别是 对角线AC上两点, .求证: .
 19. 为了了解某公司员工的年收入情况,随机抽查了公司部分员工年收入情况并绘制如图所示统计图.
19. 为了了解某公司员工的年收入情况,随机抽查了公司部分员工年收入情况并绘制如图所示统计图. (1)、请按图中数据补全条形图;(2)、由图可知员工年收入的中位数是 , 众数是;(3)、估计该公司员工人均年收入约为多少元?20. 如图,在 的正方形网格中,横、纵坐标均为整数的点叫格点.已知 , , 均在格点上.
(1)、请按图中数据补全条形图;(2)、由图可知员工年收入的中位数是 , 众数是;(3)、估计该公司员工人均年收入约为多少元?20. 如图,在 的正方形网格中,横、纵坐标均为整数的点叫格点.已知 , , 均在格点上. (1)、请建立平面直角坐标系,并直接写出C点坐标;(2)、直接写出的AC长为;(3)、在图中仅用无刻度的直尺找出AC的中点O:
(1)、请建立平面直角坐标系,并直接写出C点坐标;(2)、直接写出的AC长为;(3)、在图中仅用无刻度的直尺找出AC的中点O:第一步:找一个格点D;
第二步:连接BD,交AC于点O,O即为AC的中点;
请按步骤完成作图,并写出D点的坐标.
21. 在平面直角坐标系中,直线 分别交x轴,y轴于点A,B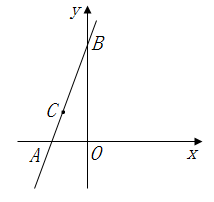 (1)、当 ,自变量x的取值范围是(直接写出结果);(2)、点 在直线 上.
(1)、当 ,自变量x的取值范围是(直接写出结果);(2)、点 在直线 上.①直接写出n的值为;
②过C点作 交x轴于点D,求直线CD的解析式.22. 已知A城有肥料200吨,B城有肥料300吨.现将这些肥料全部运往C,D两乡. C乡需要的肥料比D乡少20吨.从A城运往C,D两乡的费用分别为每吨20元和25元;从B城运往C,D两乡的费用分别为每吨15元和24元.(1)、求C,D两乡各需肥料多少吨?(2)、设从B城运往C乡的肥料为x吨,全部肥料运往C,D两乡的总运费为w元,求w与x之间的函数关系式,并直接写出自变量x的取值范围;(3)、因近期持续暴雨天气,为安全起见,从B城到C乡需要绕道运输,实际运费每吨增加了 元( ),其它路线运费不变.此时全部肥料运往C,D两乡所需最少费用为10520元,则a的值为(直接写出结果).23. 如图,在矩形ABCD中, ,E,F分别在AB,BC上. (1)、若 , .
(1)、若 , .①如图1,求证: ;
②如图2,点G为CB延长线上一点,DE的延长线交AG于H,若 ,求证: ;
(2)、如图3,若E为AB的中点, .则 的值为(结果用含n的式子表示)24. 在平面直角坐标系中,点 . (1)、直接写出直线AB的解析式;(2)、如图1,过点B的直线 交x轴于点C,若 ,求k的值;(3)、如图2,点M从A出发以每秒1个单位的速度沿AB方向运动,同时点N从O出发以每秒0.6个单位的速度沿OA方向运动,运动时间为t秒( ),过点N作 交y轴于点D,连接MD,是否存在满足条件的t,使四边形AMDN为菱形,判断并说明理由.
(1)、直接写出直线AB的解析式;(2)、如图1,过点B的直线 交x轴于点C,若 ,求k的值;(3)、如图2,点M从A出发以每秒1个单位的速度沿AB方向运动,同时点N从O出发以每秒0.6个单位的速度沿OA方向运动,运动时间为t秒( ),过点N作 交y轴于点D,连接MD,是否存在满足条件的t,使四边形AMDN为菱形,判断并说明理由.