湖北省孝感市2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2021-04-16 类型：期末考试

进入出卷网下载

一、选择题

1. 式子有意义，则x的取值范围是（）

A、x＞1 B、x＜1 C、x≥1 D、x≤1

查看试题解析
2. 一组数据2，3，5，5，4的众数、中位数分别是（　　）

A、5，4 B、5，5 C、5，4.5 D、5，3.8

查看试题解析
3. 下列四组线段中，不能构成直角三角形的是（）

A、4，5，6 B、6，8，10 C、7，24，25 D、5，3，4

查看试题解析
4. 计算 $\sqrt{24} \times \sqrt{\frac{1}{6}}$ 的结果是（）

A、4 B、± $\sqrt{4}$ C、2 D、 $\sqrt{2}$

查看试题解析
5. 菱形ABCD的对角线AC，BD相交于点O，若AC=6，菱形的周长为20，则对角线BD的长为（）

A、4 B、8 C、10 D、12

查看试题解析
6. 已知一组数据5，5，6，6，6，7，7，则这组数据的方差为（）

A、 $\frac{4}{7}$ B、 $\frac{44}{7}$ C、 $\frac{54}{7}$ D、6

查看试题解析
7. 正方形ABCD的边长为2，以AD为边作等边△ADE，则点E到BC的距离是（）

A、2+ $\sqrt{3}$ B、2- $\sqrt{3}$ C、2+ $\sqrt{3}$ ，2- $\sqrt{3}$ D、4- $\sqrt{3}$

查看试题解析
8. 如图，在Rt△ABC中，∠ACB=90°，∠A=30°，D，E，F分别为AB，AC，AD的中点，若BC=2，则EF的长度为（）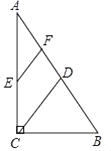

A、 $\frac{1}{2}$ B、1 C、 $\frac{3}{2}$ D、 $\sqrt{3}$

查看试题解析
9. 某通讯公司就上宽带网推出A，B，C三种月收费方式．这三种收费方式每月所需的费用y（元）与上网时间x（h）的函数关系如图所示，则下列判断错误的是（）

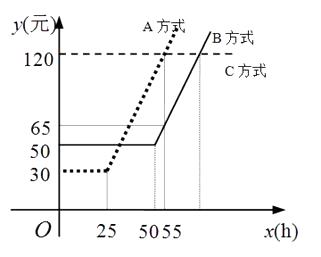A、每月上网时间不足25 h时，选择A方式最省钱 B、每月上网费用为60元时，B方式可上网的时间比A方式多 C、每月上网时间为35h时，选择B方式最省钱 D、每月上网时间超过70h时，选择C方式最省钱

查看试题解析
10. 如图，直线y=-x+m与y=nx+4n（n≠0）的交点的横坐标为-2.则下列结论：①m＜0，n＞0；②直线y=nx+4n一定经过点（-4，0）；③m与n满足m=2n-2；④当x＞-2时，nx+4n＞-x+m，其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 为选派诗词大会比赛选手，经过三轮初赛，甲、乙、丙、丁四位选手的平均成绩都是86分，方差分别是s甲²=1.5，s乙²=2.6，s丙²=3.5，s丁²=3.68，若要从中选一位发挥稳定的选手参加决赛你认为派去参赛更合适（填“甲”或“乙”或“丙”或“丁”）

查看试题解析
12. 直线y=3x-2不经过第象限.

查看试题解析
13. “我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1里=0.5千米，则该沙田的面积为平方千米.

查看试题解析
14. 如图，将矩形ABCD的四个角向内翻折后，恰好拼成一个无缝隙无重叠的四边形EFGH，EH=6cm，GH=8cm，则边AB的长是

查看试题解析
15. 如图，在平面直角坐标系中，正方形OA₁B₁C₁ ， B₁A₂B₂C₂ ， B₂A₃B₃C₃ ， …的顶点B₁ ， B₂ ， B₃ ， …在x轴上，顶点C₁ ， C₂ ， C₃ ， …在直线y=kx+b上，若正方形OA₁B₁C₁ ， B₁A₂B₂C₂的对角线OB₁=2，B₁B₂=3，则点C₃的纵坐标是.

查看试题解析

三、解答题

16. 计算： $\sqrt{45} + \sqrt{5} - 3 \sqrt{\frac{1}{3}} \times \sqrt{27}$

查看试题解析
17. 如图，▱ABCD中，AC为对角线，G为CD的中点，连接AG并廷长交BC的延长线于点F，连接DF，求证：四边形ACFD为平行四边形.

查看试题解析
18. 如图，已知四边形ABCD是平行四边形，小慧同学利用直尺和圆规进行了如下操作：①连接AC，分别以点A、C为圆心，以大于 $\frac{1}{2}$ AC的长为半径画弧，两弧相交于点P、Q；②作直线PQ，分别交BC、AC、AD于点E、O、F，连接AE、CF.根据操作结果，解答下列问题：

(1)、线段AF与CF的数量关系是

(2)、若∠BAD=120°，AE平分∠BAD，AB=8，求四边形AECF的面积.

查看试题解析
19. “中国汉字听写大会”是由中央电视台和国家语言文字工作委员会联合主办的节目，希望通过节目的播出，能吸引更多的人关注对汉字文化的学习.某校也开展了一次“汉字听写”比赛，每位参赛学生听写40个汉字.比赛结束后随机抽取部分学生的听写结果，按听写正确的汉字个数x绘制成了以下不完整的统计图.

根据以上信息回答下列问题：

(1)、本次共随机抽取了名学生进行调查，听写正确的汉字个数x在范围的人数最多；

(2)、补全频数分布直方图；

(3)、各组的组中值如下表所示.若用各组的组中值代表各组每位学生听写正确的汉字个数，求被调查学生听写正确的汉字个数的平均数；

听写正确的汉字个数x

组中值

1≤x＜11

6

11≤x＜21

16

21≤x＜31

26

31≤x＜41

36

(4)、该校共有1350名学生，如果听写正确的汉字个数不少于21个定为良好，请你估计该校本次“汉字听写”比赛达到良好的学生人数.

查看试题解析
20. 小颖用四块完全一样的长方形方砖，恰好拼成如图1所示图案，如图2，连接对角线后，她发现该图案中可以用“面积法”采用不同方案去证明勾股定理.设AE=a，DE=b，AD=c，请你找到其中一种方案证明：a²+b²=c².

查看试题解析
21. 如图，直线y= $\frac{3}{2}$ x+m与x轴交于点A（-3，0），直线y=-x+2与x轴、y轴分别交于B、C两点，并与直线y= $\frac{3}{2}$ x+m相交于点D，

(1)、点D的坐标为；

(2)、求四边形AOCD的面积；

(3)、若点P为x轴上一动点，当PD+PC的值最小时，求点P的坐标.

查看试题解析
22. 正方形ABCD的对角线AC、BD交于点O，点E、F分别在OC、OB上，且OE=OF.

(1)、如图1，若点E、F在线段OC、OB上，连接AF并延长交BE于点M，求证：AM⊥BE；

(2)、如图2，若点E、F在线段OC、OB的延长线上，连接EB并延长交AF于点M.
①∠AME的度数为；
②若正方形ABCD的边长为3 $\sqrt{2}$ ，且OC=3CE时，求BM的长.

查看试题解析

23. 一手机经销商计划购进某品牌的A型、B型、C型三款手机共60部，每款手机至少要购进8部，且恰好用完购机款61000元.设购进A型

手机x部，B型手机y部.三款手机的进价和预售价如下表：

手机型号	A型	B型	C型
进价（单位：元/部）	900	1200	1100
预售价（单位：元/部）	1200	1600	1300

(1)、用含x，y的式子表示购进C型手机的部数；

(2)、求出y与x之间的函数关系式；

(3)、假设所购进手机全部售出，综合考虑各种因素，该手机经销商在购销这批手机过程中需另外支出各种费用共1500元.

①求出预估利润P（元）与x（部）的函数关系式；

（注：预估利润P＝预售总额-购机款-各种费用）

②求出预估利润的最大值，并写出此时购进三款手机各多少部.

查看试题解析

听写正确的汉字个数x	组中值
1≤x＜11	6
11≤x＜21	16
21≤x＜31	26
31≤x＜41	36