湖北省咸宁市咸安区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2021-04-16 类型:期末考试
一、选择题
-
1. 下列式子为最简二次根式的是( )A、 B、 C、 D、2. 下列四组线段中,可以构成直角三角形的是( )A、4,5,6 B、2,3,4 C、1.5,2,2.5 D、1, ,33. 下列各式计算正确的是( )A、 B、 C、 D、4. 四边形ABCD的对角线相交于点O,且 ,那么下列条件不能判断四边形ABCD为平行四边形的是( )A、 B、 C、 D、5. 一家鞋店对上周某一品牌女鞋的销售量统计如下:
尺码/厘米
22
22.5
23
23.5
24
24.5
25
销售量/双
1
2
5
11
7
3
1
该鞋店决定本周多进一些尺码为23.5厘米的该品牌女鞋,影响鞋店决策的统计量是( )
A、方差 B、中位数 C、平均数 D、众数6. 已知一次函数y=kx+b随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )A、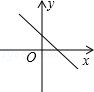 B、
B、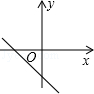 C、
C、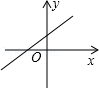 D、
D、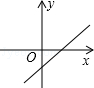 7. 如图,在菱形ABCD中,对角线AC、BD相交于点O, , ,过D作AC的平行线交BC的延长线于点E,则 的面积为( )
7. 如图,在菱形ABCD中,对角线AC、BD相交于点O, , ,过D作AC的平行线交BC的延长线于点E,则 的面积为( ) A、22 B、24 C、48 D、448. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人的距离 (米)与甲出发的时间 (分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙用16分钟追上甲;③乙走完全程用了30分钟;④乙到达终点时甲离终点还有360米.其中正确的结论有( )
A、22 B、24 C、48 D、448. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟.在整个步行过程中,甲、乙两人的距离 (米)与甲出发的时间 (分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙用16分钟追上甲;③乙走完全程用了30分钟;④乙到达终点时甲离终点还有360米.其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 4的算术平方根是 .10. 若在实数范围内有意义,则x的取值范围是 .
11. 已知 是一次函数,则 .12. 若一组数据1,3,x,5,4,6的平均数是4,则这组数据的中位数是.13. 如图,直线y=kx+b(k≠0)与x轴交于点(﹣4,0),则关于x的方程kx+b=0的解为x= .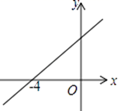 14. 如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点G的坐标为.
14. 如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点G的坐标为. 15. 如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是.
15. 如图,菱形ABCD的边长为4,∠BAD=120°,点E是AB的中点,点F是AC上的一动点,则EF+BF的最小值是.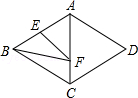 16. 如图,正方形ABCD中, ,点E在边C上,且 .将 沿AE对折至 ,延长EF交边BC于点G,连接AG、CF.则下列结论:① :② ;③ :④ .其中正确的有(把你认为正确结论的序号都填上)
16. 如图,正方形ABCD中, ,点E在边C上,且 .将 沿AE对折至 ,延长EF交边BC于点G,连接AG、CF.则下列结论:① :② ;③ :④ .其中正确的有(把你认为正确结论的序号都填上)
三、解答题
-
17.(1)、(2)、18. 已知一次函数 的图象与正比例函数 的图象的交点A的纵坐标是4.且与x轴的交点B的横坐标是-3
 (1)、求这个一次函数的解析式;(2)、直接写出 时 的取值范围.19. 如图,已知 , , , , ,试求阴影部分的面积.
(1)、求这个一次函数的解析式;(2)、直接写出 时 的取值范围.19. 如图,已知 , , , , ,试求阴影部分的面积. 20. 中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了解学生对四大名著的阅读情况,就“四大古典名著”你读完了几部的问题在全校900名学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
20. 中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了解学生对四大名著的阅读情况,就“四大古典名著”你读完了几部的问题在全校900名学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
请根据以上信息,解决下列问题
(1)、本次调查被调查的学生名,学生阅读名著数量(部)的众数是 , 中位数是;(2)、扇形统计图中“1部”所在扇形的圆心角为度;(3)、请将条形统计图补充完整;(4)、试估算全校大约有多少学生读完了3部以上(含3部)名著.21. 如图,在 中,点O是AC边的一个动点,过点O作 ,交 的平分线于点E,交 的外角平分线于点F, (1)、求证: ;(2)、当点O位于AC边的什么位置时四边形AECF是矩形?并说明理由.22. 某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件 种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元.设生产A种产品的件数为x(件),生产A、B两种产品所获总利润为y(元)(1)、试写出y与x之间的函数关系式:(2)、求出自变量x的取值范围;(3)、利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?23. 某班“数学兴趣小组”对函数 的图象和性质进行了探究,过程如下,请补充完整.(1)、自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
(1)、求证: ;(2)、当点O位于AC边的什么位置时四边形AECF是矩形?并说明理由.22. 某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品共50件.已知生产一件A种产品需用甲种原料9千克、乙种原料3千克,可获利润700元;生产一件 种产品需用甲种原料4千克、乙种原料10千克,可获利润1200元.设生产A种产品的件数为x(件),生产A、B两种产品所获总利润为y(元)(1)、试写出y与x之间的函数关系式:(2)、求出自变量x的取值范围;(3)、利用函数的性质说明哪种生产方案获总利润最大?最大利润是多少?23. 某班“数学兴趣小组”对函数 的图象和性质进行了探究,过程如下,请补充完整.(1)、自变量x的取值范围是全体实数,x与y的几组对应值列表如下:x
…
-3
-2
-1
0
1
2
3
4
5
…
y
…
4
m
2
1
0
1
2
3
4
…
其中, .
(2)、根据上表的数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分. (3)、观察图象,写出该函数的两条性质:
(3)、观察图象,写出该函数的两条性质:①
②
(4)、进一步探究函数图象发现:①方程 的解是.
②方程 的解是.
③关于x的方程 有两个不相等实数根,则a的取值范围是.
24. 如图,在正方形ABCD中,点E、F是正方形内两点, , ,为探索这个图形的特殊性质,某数学兴趣小组经历了如下过程: (1)、在图1中,连接BD,且
(1)、在图1中,连接BD,且①求证:EF与BD互相平分;
②求证: ;
(2)、在图2中,当 ,其它条件不变时, 是否成立?若成立,请证明:若不成立,请说明理由. (3)、在图3中,当 , , 时,求 之长.
(3)、在图3中,当 , , 时,求 之长.