湖北省武汉市硚口区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2021-04-16 类型:期末考试
一、选择题
-
1. 函数y= 的自变量的取值范围是( )A、x≥2 B、x<2 C、x>2 D、x≤22. 下列计算正确的是( )A、 B、 C、 D、3. 一组数据3、-2、0、1、4的中位数是( )A、0 B、1 C、-2 D、44. 、 、 为 三边,下列条件不能判断它是直角三角形的是( )A、 B、 , , C、 D、 , , ( 为正整数)5. 如图,直线 交直线 于点 ,则关于 的不等式 的解集为( )
 A、 B、 C、 D、6. 下列是假命题的是( )A、平行四边形对边平行 B、矩形的对角线相等 C、两组对边分别平行的四边形是平行四边形 D、对角线相等的四边形是矩形7. 正比例函数 的图象经过点 , ,当 时, ,则 的取值范围是( )A、 B、 C、 D、8. 下列式子:① ;② ;③ ;④ .其中y是x的函数的个数是( )A、1 B、2 C、3 D、49. 如图,在平面直角坐标系中, , , ,…都是等腰直角三角形,其直角顶点 , , ,…均在直线 上.设 , , ,…的面积分别为 , , ,…,根据图形所反映的规律, ( )
A、 B、 C、 D、6. 下列是假命题的是( )A、平行四边形对边平行 B、矩形的对角线相等 C、两组对边分别平行的四边形是平行四边形 D、对角线相等的四边形是矩形7. 正比例函数 的图象经过点 , ,当 时, ,则 的取值范围是( )A、 B、 C、 D、8. 下列式子:① ;② ;③ ;④ .其中y是x的函数的个数是( )A、1 B、2 C、3 D、49. 如图,在平面直角坐标系中, , , ,…都是等腰直角三角形,其直角顶点 , , ,…均在直线 上.设 , , ,…的面积分别为 , , ,…,根据图形所反映的规律, ( ) A、 B、 C、 D、10. 如图,矩形 中, 是 边的中点, 是 边上一点, , , ,则线段 的长为( )
A、 B、 C、 D、10. 如图,矩形 中, 是 边的中点, 是 边上一点, , , ,则线段 的长为( )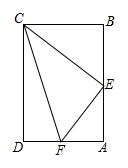 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 化简 的结果是.12. 一组数据15、13、14、13、16、13的众数是 , 中位数是.13. 已知菱形两条对角线的长分别为4和6,则菱形的边长为.14. 一个有进水管与出水管的容器,从某时刻开始的4分内只进水不出水,在随后的若干分内既进水又出水,之后只有出水不进水,每分钟的进水量和出水量是两个常数,容器内的水量 (单位:升)与时间 (单位:分)之间的关系如图所示,则进水速度是升/分,出水速度是升/分, 的值为.
 15. 如图,已知 , , ,当 时, .
15. 如图,已知 , , ,当 时, . 16. 如图,正方形 中,点 在 上, 交 、 于点 、 ,点 、 分别为 、 的中点,连接 、 ,若 , ,则 .
16. 如图,正方形 中,点 在 上, 交 、 于点 、 ,点 、 分别为 、 的中点,连接 、 ,若 , ,则 .
三、解答题
-
17. 一次函数 的图象经过 和 两点.(1)、求一次函数的解析式.(2)、当 时,求 的值.18. 如图, , 平分 ,交 于点 , 平分 ,交 于点 ,连接 .求证:四边形 是菱形.
 19. 某市教育局为了了解初二学生每学期参加综合实践活动的情况,随机抽样调查了某校初二学生一个学期参加综合实践活动的天数,并用得到的数据绘制了两幅不完整的统计图.请你根据图中提供的信息,解答下列问题:
19. 某市教育局为了了解初二学生每学期参加综合实践活动的情况,随机抽样调查了某校初二学生一个学期参加综合实践活动的天数,并用得到的数据绘制了两幅不完整的统计图.请你根据图中提供的信息,解答下列问题: (1)、扇形统计图中 的值为 , 的值为.(2)、扇形统计图中参加综合实践活动天数为6天的扇形的圆心角大小为.(3)、请你估计该市初二学生每学期参加综合实践活动的平均天数大约是多少天(精确到个位)?(4)、若全市初二学生共有90000名学生,估计有多少名学生一个学期参加综合社会活动的天数不少于5天?20.
(1)、扇形统计图中 的值为 , 的值为.(2)、扇形统计图中参加综合实践活动天数为6天的扇形的圆心角大小为.(3)、请你估计该市初二学生每学期参加综合实践活动的平均天数大约是多少天(精确到个位)?(4)、若全市初二学生共有90000名学生,估计有多少名学生一个学期参加综合社会活动的天数不少于5天?20. (1)、如图1,方格纸中的每个小方格都是边长为1个单位的正方形, 的顶点以及点 均在格点上.
(1)、如图1,方格纸中的每个小方格都是边长为1个单位的正方形, 的顶点以及点 均在格点上.①直接写出 的长为_▲_;
②画出以 为边, 为对角线交点的平行四边形 .
(2)、如图2,画出一个以 为对角线,面积为6的矩形 ,且 G 和 均在格点上( 、 、 、 按顺时针方向排列).(3)、如图3,正方形 中, 为 上一点,在线段 上找一点 ,使得 .(要求用无刻度的直尺画图,不准用圆规,不写作法,保留画图痕迹)21. 如图1,在平画直角坐标系中,直线 交 轴于点 ,交 轴于点 ,将直线 沿 轴向右平移2个单位长度交 轴于 ,交 轴于 ,交直线 于 . (1)、直接写出直线 的解析式为 , .(2)、在直线 上存在点 ,使 是 的中线,求点 的坐标;(3)、如图2,在 轴正半轴上存在点 ,使 ,求点 的坐标.22. 某手机店销售10部A型和20部B型手机的利润为4000元,销售20部A型和10部B型手机的利润为3500元.(1)、求每部A型手机和B型手机的销售利润;(2)、该手机店计划一次购进A,B两种型号的手机共100部,其中B型手机的进货量不超过A型手机的2倍,设购进A型手机x部,这100部手机的销售总利润为y元.
(1)、直接写出直线 的解析式为 , .(2)、在直线 上存在点 ,使 是 的中线,求点 的坐标;(3)、如图2,在 轴正半轴上存在点 ,使 ,求点 的坐标.22. 某手机店销售10部A型和20部B型手机的利润为4000元,销售20部A型和10部B型手机的利润为3500元.(1)、求每部A型手机和B型手机的销售利润;(2)、该手机店计划一次购进A,B两种型号的手机共100部,其中B型手机的进货量不超过A型手机的2倍,设购进A型手机x部,这100部手机的销售总利润为y元.①求y关于x的函数关系式;
②该手机店购进A型、B型手机各多少部,才能使销售总利润最大?
(3)、在(2)的条件下,该手机店实际进货时,厂家对A型手机出厂价下调 元,且限定手机店最多购进A型手机70部,若手机店保持同种手机的售价不变,设计出使这 部手机销售总利润最大的进货方案.23. 已知正方形 的边长为4, 、 分别为直线 、 上两点. (1)、如图1,点 在 上,点 在 上, ,求证: .(2)、如图2,点 为 延长线上一点,作 交 的延长线于 ,作 于 ,求 的长.(3)、如图3,点 在 的延长线上, ,点 在 上, ,直线 交 于 ,连接 ,设 的面积为 ,直接写出 与 的函数关系式.24. 如图1,已知直线 : 交 轴于 ,交 轴于 .
(1)、如图1,点 在 上,点 在 上, ,求证: .(2)、如图2,点 为 延长线上一点,作 交 的延长线于 ,作 于 ,求 的长.(3)、如图3,点 在 的延长线上, ,点 在 上, ,直线 交 于 ,连接 ,设 的面积为 ,直接写出 与 的函数关系式.24. 如图1,已知直线 : 交 轴于 ,交 轴于 . (1)、直接写出 的值为.(2)、如图2, 为 轴负半轴上一点,过 点的直线 : 经过 的中点 ,点 为 轴上一动点,过 作 轴分别交直线 、 于 、 ,且 ,求 的值.(3)、如图3,已知点 ,点 为直线 右侧一点,且满足 ,求点 坐标.
(1)、直接写出 的值为.(2)、如图2, 为 轴负半轴上一点,过 点的直线 : 经过 的中点 ,点 为 轴上一动点,过 作 轴分别交直线 、 于 、 ,且 ,求 的值.(3)、如图3,已知点 ,点 为直线 右侧一点,且满足 ,求点 坐标.