湖北省武汉市江夏区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2021-04-16 类型:期末考试
一、选择题
-
1. 函数 中自变量 的取值范围是( )A、 B、 C、 D、全体实数2. 下列计算正确的是( )A、 B、 C、 D、3. 一次函数 的图象不经过( )象限A、第一 B、第二 C、第三 D、第四4. 下列判断错误的是( )A、两组对边分别相等的四边形是平行四边形 B、四个内角都相等的四边形是矩形 C、四条边都相等的四边形是菱形 D、两条对角线垂直且平分的四边形是正方形5. 某小组5名同学在一周内参加家务劳动的时间如下表,关于“劳动时间”的这组数据,以下说法正确的是( ).
劳动时间(小时)
3
3.2
4
4.5
人数
1
1
2
1
A、中位数是4,平均数是3.74 B、中位数是4,平均数是3.75 C、众数是4,平均数是3.75 D、众数是2,平均数是3.86. 如图,四边形 是菱形, 经过点 、 、 ,与 相交于点 ,连接 、 .若 ,则 的度数为( ) A、 B、 C、 D、7. 如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B
A、 B、 C、 D、7. 如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B C
C  D作匀速运动,那么△ABP的面积
D作匀速运动,那么△ABP的面积  与点P运动的路程
与点P运动的路程  之间的函数图象大致是( ).
之间的函数图象大致是( ).  A、
A、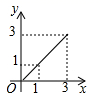 B、
B、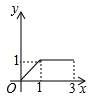 C、
C、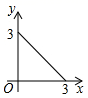 D、
D、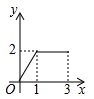 8. 某种出租车的收费标准是:起步价8元(即距离不超过 ,都付8元车费),超过 以后,每增加 ,加收1.2元(不足 按 计).若某人乘这种出租车从甲地到乙地经过的路程是 ,共付车费14元,那么 的最大值是( ).A、6 B、7 C、8 D、99. 如图,△ABC中,AB=6,AC=4,AD是∠BAC的外角平分线,CD⊥AD于D,且点E是BC的中点,则DE为( )
8. 某种出租车的收费标准是:起步价8元(即距离不超过 ,都付8元车费),超过 以后,每增加 ,加收1.2元(不足 按 计).若某人乘这种出租车从甲地到乙地经过的路程是 ,共付车费14元,那么 的最大值是( ).A、6 B、7 C、8 D、99. 如图,△ABC中,AB=6,AC=4,AD是∠BAC的外角平分线,CD⊥AD于D,且点E是BC的中点,则DE为( )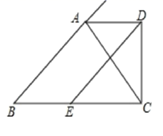 A、8.5 B、8 C、7.5 D、510. 在平面直角坐标系中,线段AB两端点的坐标分别为A(1,0),B(3,2).将线段AB平移后,A、B的对应点的坐标可以是( )A、(1,−1),(−1,−3) B、(1,1),(3,3) C、(−1,3),(3,1) D、(3,2),(1,4)11. ① ;② ;③ .12. 把直线 向上平移2个单位得到的直线解析式为:.13. 化简: .14. 如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是.
A、8.5 B、8 C、7.5 D、510. 在平面直角坐标系中,线段AB两端点的坐标分别为A(1,0),B(3,2).将线段AB平移后,A、B的对应点的坐标可以是( )A、(1,−1),(−1,−3) B、(1,1),(3,3) C、(−1,3),(3,1) D、(3,2),(1,4)11. ① ;② ;③ .12. 把直线 向上平移2个单位得到的直线解析式为:.13. 化简: .14. 如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是.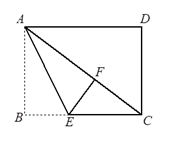 15. 函数 与 的图象恰有两个公共点,则实数m的取值范围是.16. 如图.△ABC中,AC的垂直平分线分别交AC、AB于点D.F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是
15. 函数 与 的图象恰有两个公共点,则实数m的取值范围是.16. 如图.△ABC中,AC的垂直平分线分别交AC、AB于点D.F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是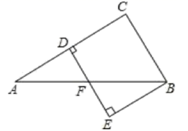
二、解答题
-
17. 计算:(1)、(2)、18.
如图,在▱ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.
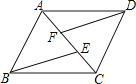 19. 某学校欲招聘一名新教师,对甲、乙、丙三名应试者进行了面试、笔试和才艺三个方面的量化考核,他们的各项得分(百分制)如下表所示:
19. 某学校欲招聘一名新教师,对甲、乙、丙三名应试者进行了面试、笔试和才艺三个方面的量化考核,他们的各项得分(百分制)如下表所示:应试者
面试成绩
笔试成绩
才艺
甲
83
79
90
乙
85
80
75
丙
80
90
73
(1)、根据三项得分的平均分,从高到低确定应聘者的排名顺序;(2)、学校规定:笔试、面试、才艺得分分别不得低于80分、80分、70分,并按照60%、30%、10%的比例计入个人总分,请你说明谁会被录用?20. 如图,在由边长为1个单位的长度的小正方形组成的网格图中,已知点O及△ABC的顶点均为网格线的交点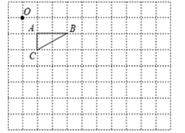 (1)、 在给定网格中,以O为位似中心,将△ABC放大为原来的三倍,得到请△A′B′C′,请画出△A′B′C′;(2)、 B′C′的长度为单位长度,△A′B′C′的面积为平方单位。21. 如图,菱形ABCD中,E为对角线BD的延长线上一点.
(1)、 在给定网格中,以O为位似中心,将△ABC放大为原来的三倍,得到请△A′B′C′,请画出△A′B′C′;(2)、 B′C′的长度为单位长度,△A′B′C′的面积为平方单位。21. 如图,菱形ABCD中,E为对角线BD的延长线上一点.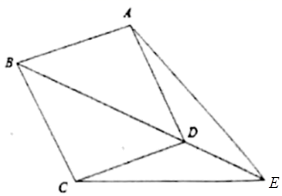 (1)、求证:AE=CE;(2)、若BC=6,AE=10,∠BAE=120°,求DE的长.22. 如图,直线 与 轴交于点 ,与 轴交于点 ,与直线 交于点 ,点 的横坐标为3.
(1)、求证:AE=CE;(2)、若BC=6,AE=10,∠BAE=120°,求DE的长.22. 如图,直线 与 轴交于点 ,与 轴交于点 ,与直线 交于点 ,点 的横坐标为3.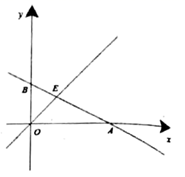 (1)、直接写出b值;(2)、当x取何值时, ?(3)、在x轴上有一点 ,过点p作x轴的垂线,与直线 交于点C,与直线 交于点 ,若 ,求m的值.23. 列方程(组)及不等式(组)解应用题:
(1)、直接写出b值;(2)、当x取何值时, ?(3)、在x轴上有一点 ,过点p作x轴的垂线,与直线 交于点C,与直线 交于点 ,若 ,求m的值.23. 列方程(组)及不等式(组)解应用题:水是生命之源.为了鼓励市民节约用水,江夏区水务部门实行居民用水阶梯式计量水价政策;若居民每户每月用水量不超过10立方米,每立方米按现行居民生活用水水价收费(现行居民生活用水水价=基本水价+污水处理费);若每户每月用水量超过10立方米,则超过部分每立方米在基本水价基础上加价100%,但每立方米污水处理费不变.
下面表格是某居民小区4月份甲、乙两户居民生活用水量及缴纳生活用水水费的情况统计:
4月份居民用水情况统计表
(注:污水处理的立方数=实际生活用水的立方数)
用水量(立方米)
缴纳生活用水费用(元)
甲用户
8
27.6
乙用户
12
46.3
(1)、求每立方米的基本水价和每立方米的污水处理费各是多少?(2)、设这个小区某居民用户5月份用水x立方米,需要缴纳的生活用水水费为y元.若他5月份生活用水水费计划不超过64元,该用户5月份最多可用水多少立方米?24. 在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N.
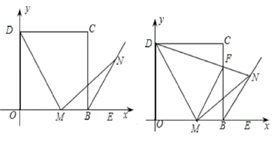 (1)、写出点C的坐标;(2)、求证:MD=MN;(3)、连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明
(1)、写出点C的坐标;(2)、求证:MD=MN;(3)、连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明