湖北省武汉市江岸区（洪山)联考2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2021-04-16 类型：期末考试

进入出卷网下载

一、选择题

1. 二次根式 $\sqrt{a - 2}$ 在实数范围内有意义，则 $a$ 的取值范围是（）

A、 $a \leq 2$ B、 $a \geq 2$ C、 $a < 2$ D、 $a > 2$

查看试题解析
2. 下列各式中，化简后能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{12}$ B、 $\sqrt{8}$ C、 $\sqrt{\frac{2}{3}}$ D、 $\sqrt{0.2}$

查看试题解析
3. 一组数据2,3,4,6,6,7的众数是（）

A、3 B、4 C、5 D、6

查看试题解析
4. 已知一次函数 $y = (k - 1) x$ . 若 $y$ 随 $x$ 的增大而增大，则 $k$ 的取值范围是（）

A、 $k < 1$ B、 $k > 1$ C、 $k < 0$ D、 $k > 0$

查看试题解析
5. 在 $Rt$ △ $A B C$ 中， $D$ 为斜边 $A B$ 的中点，且 $B C = 3$ ， $A C = 4$ ，则线段 $C D$ 的长是（）

A、 $2$ B、 $3$ C、 $\frac{5}{2}$ D、 $5$

查看试题解析
6. 如图，在点M，N，P，Q中，一次函数y＝kx＋2（k＜0）的图象不可能经过的点是（）

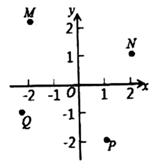A、M B、N C、P D、Q

查看试题解析
7. 把直线y＝﹣2x向上平移后得到直线AB ，若直线AB经过点（m ， n），且2m+n＝8，则直线AB的表达式为（）

A、y＝﹣2x+4 B、y＝﹣2x+8 C、y＝﹣2x﹣4 D、y＝﹣2x﹣8

查看试题解析
8. 如图，在菱形ABCD中，E，F别是AB，AC的中点，若 $E F = 2$ ， $A C = 6$ ，则菱形ABCD的面积为（）

A、 $6 \sqrt{7}$ B、12 C、15 D、 $10 \sqrt{5}$

查看试题解析
9. 如图，将5个全等的阴影小正方形摆放得到边长为1的正方形ABCD，中间小正方形的各边的中点恰好为另外4个小正方形的一个顶点，小正方形的边长为 $\frac{a - \sqrt{2}}{b}$ （a、b为正整数），则 $a + b$ 的值为（）

A、10 B、11 C、12 D、 $13$ 13

查看试题解析
10. 如图，已知平行四边形ABCD， $A B = 6$ ， $B C = 9$ ， $∠ A = 120 °$ ，点P是边AB上一动点，作 $P E ⊥ B C$ 于点E，作 $∠ E P F = 120 °$ （PF在PE右边）且始终保持 $P E + P F = 3 \sqrt{3}$ ，连接CF、DF，设 $m = C F + D F$ ，则m满足（）

A、 $m \geq 3 \sqrt{13}$ B、 $m \geq 6 \sqrt{3}$ C、 $3 \sqrt{13} \leq m < 9 + 3 \sqrt{7}$ D、 $3 \sqrt{3} + 3 \sqrt{7} < m < 3 \sqrt{7} + 9$

查看试题解析
11. 若正比例函数y=kx的图象经过点（1，2），则k= ．

查看试题解析
12. 已知 $y = \sqrt{x - 1} - \sqrt{1 - x}$ ，则 $x + y$ 的值为.

查看试题解析

13. 数学兴趣小组的甲、乙、丙、丁四位同学进行还原魔方练习，下表记录了他们10次还原魔方所用时间的平均值

\bar{x}

与方差

S^{2}

：

	甲	乙	丙	丁
$\bar{x}$ （秒）	30	30	28	28
$S^{2}$	1.21	1.05	1.21	1.05

要从中选择一名还原魔方用时少又发挥稳定的同学参加比赛，应该选择同学.

查看试题解析

14. 小明租用共享单车从家出发，匀速骑行到相距2400米的图书馆还书.小明出发的同时，他的爸爸以每分钟96米的速度从图书馆沿同一条道路步行回家，小明在图书馆停留了2分钟后沿原路按原速返回.设他们出发后经过t（分）时，小明与家之间的距离为 $s_{1}$ （米），小明爸爸与家之间的距离为 $s_{2}$ （米），图中折线OABD、线段EF分别表示 $s_{1}$ 、 $s_{2}$ 与t之间的函数关系的图象.小明从家出发，经过分钟在返回途中追上爸爸.

查看试题解析
15. 如图，已知 $△ A B C$ 是等边三角形，点D在边BC上，以AD为边向左作等边 $△ A D E$ ，连结BE，作 $B F ∥ A E$ 交AC于点F，若 $A F = 2$ ， $C F = 4$ ，则 $A E =$ .

查看试题解析
16. 已知：正方形ABCD，E为平面内任意一点，连接DE，将线段DE绕点D顺时针旋转 $90 °$ 得到DG，当点B，D，G在一条直线时，若 $A D = 4$ ， $D G = 2 \sqrt{2}$ ，则 $C E =$ .

查看试题解析

二、解答题

17. 计算： $(2 \sqrt{3} + \sqrt{2}) (2 \sqrt{3} - \sqrt{2})$

查看试题解析
18. 如图，已知正方形ABCD，点E、F分别在边BC、CD上，若 $B E = C F$ ，判断AE、BF的关系并证明.

查看试题解析

19. 某校为了弘扬中华传统文化，了解学生整体阅读能力，组织全校的1000名学生进行一次阅读理解大赛.从中抽取部分学生的成绩进行统计分析，根据测试成绩绘制了频数分布表和频数分布直方图：

分组/分	频数	频率
50≤x＜60	6	0.12
60≤x＜70	a	0.28
70≤x＜80	16	0.32
80≤x＜90	10	0.20
90≤x≤100	4	0.08

(1)、频数分布表中的

a =

；

(2)、将上面的频数分布直方图补充完整；

(3)、如果成绩达到90及90分以上者为优秀，可推荐参加决赛，估计该校进入决赛的学生大约有人.

查看试题解析

20. 如图，在平面直角坐标系中，直线AB： $y = k x + b$ 经过 $A (\frac{5}{2} ， - 1)$ ，分别交x轴、直线 $y = x$ 、y轴于点B，P，C，已知B(2，0).

(1)、求直线AB的解析式；

(2)、直线y=m分别交直线AB于点E、交直线y=x于点F，若点F在点E的右边，说明m满足的条件.

查看试题解析
21. 如图，在 $8 \times 8$ 的网格中，网格线的公共点称为格点.已知格点 $A (1 ， 1)$ 、 $B (6 ， 1)$ ，如图所示线段AC上存在另外一个格点.

(1)、建立平面直角坐标系，并标注x轴、y轴、原点；

(2)、直接写出线段AC经过的另外一个格点的坐标：；

(3)、用无刻度的直尺画图，运用所学的三角形全等的知识画出经过格点D的射线BD，使 $B D ⊥ A C$ （保留画图痕迹），并直接写出点 $D$ 的坐标：.

查看试题解析
22. 武汉某文化旅游公司为了在军运会期间更好地宣传武汉，在工厂定制了一批具有浓郁的武汉特色的商品.为了了解市场情况，该公司向市场投放A，B型商品共250件进行试销，A型商品成本价160元/件，B商品成本价150元/件，其中A型商品的件数不大于B型的件数，且不小于80件，已知A型商品的售价为240元／件，B型商品的售价为220元／件，且全部售出.设投放A型商品x件，该公司销售这批商品的利润y元.

(1)、直接写出y与x之间的函数关系式：；

(2)、为了使这批商品的利润最大，该公司应该向市场投放多少件A型商品？最大利润是多少？

(3)、该公司决定在试销活动中每售出一件A型商品，就从一件A型商品的利润中捐献慈善资金a元，当该公司售完这250件商品并捐献资金后获得的最大收益为18000元时，求a的值.

查看试题解析
23. 已知正方形ABCD，直线l垂直平分线段BC，点M是直线l上一动点，连结BM，将线段BM绕点M顺时针旋转90°得到线段MN，连接BN.

(1)、如图1，点M在正方形内部，连接NC，求 $∠ B C N$ 的度数；

(2)、如图2，点M在正方形内部，连接ND，若 $N D ⊥ M N$ ，求 $\frac{N D^{2}}{C D^{2}}$ 的值.

查看试题解析
24. 已知直线 $l_{1}$ ： $y = k x + 2 k$ 与函数 $y = | x - a | + a$ .

(1)、直线 $l_{1}$ 经过定点P，直接写出点P的坐标：；

(2)、当 $a = 1$ 时，直线 $l_{1}$ 与函数 $y = | x - a | + a$ 的图象存在唯一的公共点，在图1中画出 $y = | x - a | + a$ 的函数图象并直接写出k满足的条件；

(3)、如图2，在平面直角坐标系中存在正方形ABCD，已知 $A (2 ， 2)$ 、 $C (- 2 ， - 2)$ .请认真思考函数 $y = | x - a | + a$ 的图象的特征，解决下列问题：
①当 $a = - 1$ 时，请直接写出函数 $y = | x - a | + a$ 的图象与正方形ABCD的边的交点坐标：；
②设正方形ABCD在函数 $y = | x - a | + a$ 的图象上方的部分的面积为S，求出S与a的函数关系式.

查看试题解析