湖北省武汉市汉阳区2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2021-04-16 类型：期末考试

进入出卷网下载

一、选择题

1. 4的算术平方根是（）

A、 $\pm 2$ B、2 C、-2 D、 $\pm \sqrt{4}$

查看试题解析
2. 使 $\sqrt{x - 2}$ 有意义的x的取值范围是（）

A、 $x \neq 2$ B、 $x \geq 2$ C、 $x > 2$ D、 $x \geq 0$

查看试题解析
3. 五名女生的体重（单位：kg）分别为：37、40、38、42、42，这组数据的众数和中位数分别是（）

A、2、40 B、42、38 C、40、42 D、42、40

查看试题解析

4. 八（1）班45名同学一天的生活费用统计如下表：

生活费（元）	10	15	20	25	30
学生人数（人）	3	9	15	12	6

则这45名同学一天的生活费用中，平均数是（）

A、15 B、20 C、21 D、25

查看试题解析

5. 下列函数中为正比例函数的是（）

A、 $y = 3 x^{2}$ B、 $y = \frac{3}{x}$ C、 $y = \frac{x}{3}$ D、 $y = 6 x + 1$

查看试题解析
6. 若以二元一次方程x+2y﹣b=0的解为坐标的点（x，y）都在直线y=﹣ $\frac{1}{2}$ x+b﹣1上，则常数b=（）

A、 $\frac{1}{2}$ B、2 C、﹣1 D、1

查看试题解析
7. 一次函数y=kx﹣1的图象经过点P，且y的值随x值的增大而增大，则点P的坐标可以为（）

A、（﹣5，3） B、（1，﹣3） C、（2，2） D、（5，﹣1）

查看试题解析
8. “赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a，较短直角边长为b．若ab=8，大正方形的面积为25，则小正方形的边长为（）

A、9 B、6 C、4 D、3

查看试题解析
9. 如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于E，F，连接PB，PD．若AE=2，PF=8．则图中阴影部分的面积为（）

A、10 B、12 C、16 D、18

查看试题解析
10. 甲、乙两车从A地出发，匀速驶向B地.甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶.乙车先到达B地并停留1h后，再以原速按原路返回，直至与甲车相遇.在此过程中，两车之间的距离y（km）与乙车行驶时间x（h）之间的函数关系如图所示.下列说法：①乙车的速度是120km/h；②m＝160；③点H的坐标是（7，80）；④n＝7.5.其中说法正确的是（）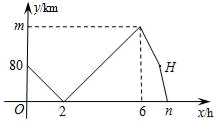

A、①②③ B、①②④ C、①③④ D、①②③④

查看试题解析

二、填空题

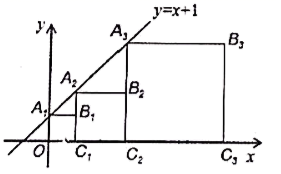
11. 计算 $\sqrt{27} - \sqrt{12}$ 的结果是.

查看试题解析
12. 一组数据为0，1，2，3，4，则这组数据的方差是．

查看试题解析
13. 将直线 $y = 3 x - 3$ 向右平移2个单位，所得的直线的与坐标轴所围成的面积是.

查看试题解析
14. 以正方形ABCD的边AD作等边△ADE，则∠BEC的度数是．

查看试题解析
15. 正方形 $A_{1} B_{1} C_{1} O$ ， $A_{2} B_{2} C_{2} C_{1}$ ， $A_{3} B_{3} C_{3} C_{2}$ ，...按如图的方式放置，点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ...和点 $C_{1}$ ， $C_{2}$ ， $C_{3}$ ...分别在直线 $y = x + 1$ 和x轴上，则点 $B_{2019}$ 的坐标为.

查看试题解析
16. 如图，已知 $∠ X O Y = 60 °$ ，点 $A$ 在边 $O X$ 上， $O A = 2$ .过点 $A$ 作 $A C ⊥ O Y$ 于点 $C$ ，以 $A C$ 为一边在 $∠ X O Y$ 内作等边 $Δ A B C$ ，点 $P$ 是 $Δ A B C$ 围成的区域（包括各边）内的一点，过点 $P$ 作 $P D / / O Y$ 交 $O X$ 于点 $D$ ，作 $P E / / O X$ 交 $O Y$ 于点 $E$ .设 $O D = a$ ， $O E = b$ ，则 $a + 2 b$ 最大值是.

查看试题解析

三、解答题

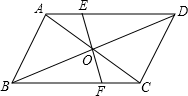
17. 一次函数图象经过（3，8）和（5，12）两点，求一次函数解析式．

查看试题解析
18. 如图，平行四边形ABCD的对角线AC，BD相交于点O，EF过点O且与AD，BC分别相交于点E，F.求证：OE=OF.

查看试题解析
19. 某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原始分均为100分.前3名选手的得分如下：根据规定，笔试成绩和面试成绩分别按一定的百分比折合成综合成绩（综合成绩的满分仍为100分），现得知1号选手的综合成绩为87分.

序号

1

2

3

笔试成绩/分

90

92

84

面试成绩/分

85

88

86

(1)、求笔试成绩和面试成绩各占的百分比：

(2)、求出其余两名选手的综合成绩，并以综合成绩排序确定这三名选手的名次。

查看试题解析
20. 现将三张形状、大小完全相同的平行四边形透明纸片分别放在方格纸中，方格纸中的每个小正方形的边长均为1，并且平行四边形纸片的每个顶点与小正方形的顶点重合(如图①、图②、图③).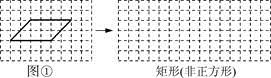

图②矩形(正方形)

，

分别在图①、图②、图③中，经过平行四边形纸片的任意一个顶点画一条裁剪线，沿此裁剪线将平行四边形纸片裁成两部分，并把这两部分重新拼成符合下列要求的几何图形.

要求：
（1）在左边的平行四边形纸片中画一条裁剪线，然后在右边相对应的方格纸中，按实际大小画出所拼成的符合要求的几何图形.
（2）裁成的两部分在拼成几何图形时要互不重叠且不留空隙.
（3）所画出的几何图形的各顶点必须与小正方形的顶点重合.

查看试题解析
21. 如图，将矩形纸片ABCD（ $A D > A B$ ）折叠，使点C刚好落在线段AD上，且折痕分别与边BC，AD相交于点E，F，设折叠后点C，D的对应点分别为点G，H.

(1)、判断四边形CEGF的形状，并证明你的结论；

(2)、若 $A B = 4$ ，且四边形CEGF的面积20，求线段EF的长.

查看试题解析
22. 某网店销售单价分别为60元/筒、45元/筒的甲、乙两种羽毛球.根据消费者需求，该网店决定用不超过8780元购进甲、乙两种羽毛球共 $200$ 简.且甲种羽毛球的数量大于乙种羽毛球数量的 $\frac{3}{5}$ .已知甲、乙两种羽毛球的进价分别为50元/筒、40元/筒。若设购进甲种羽毛球m简.

(1)、该网店共有几种进货方案?

(2)、若所购进羽毛球均可全部售出，求该网店所获利润 $W$ （元）与甲种羽毛球进货量 $m$ （简）之间的函数关系式，并求利润的最大值

查看试题解析
23. 如图，长方形ABCD中，点P沿着边按 $B \to C \to D \to A$ .方向运动，开始以每秒m个单位匀速运动、a秒后变为每秒2个单位匀速运动，b秒后恢复原速匀速运动，在运动过程中， $Δ A B P$ 的面积S与运动时间t的函数关系如图所示.

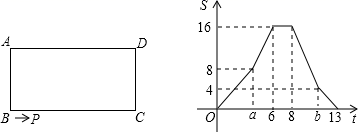(1)、直接写出长方形的长和宽；

(2)、求m，a，b的值；

(3)、当P点在D边上时，直接写出S与t的函数解析式.

查看试题解析
24. 如图，在边长为 $\sqrt{2}$ 正方形ABCD中，点O是对角线AC的中点，E是线段OA上一动点（不包括两个端点），连接BE

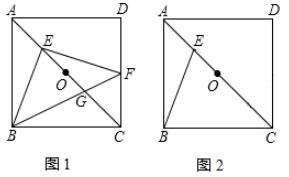(1)、如图1，过点E作 $E F ⊥ B E$ 交CD于点F，连接BF交AC于点G
①求证： $B E = E F$ ；

②设 $A E = x$ ， $C G = y$ ，求y与x的函数关系式，并写出自变量x的取值范围.

(2)、在如图2中，请用无刻度的直尺作出一个以BE为边的菱形.

查看试题解析

序号	1	2	3
笔试成绩/分	90	92	84
面试成绩/分	85	88	86