湖北省武汉市蔡甸区2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2021-04-16 类型：期末考试

进入出卷网下载

一、选择题

1. 化简 $\sqrt{18}$ 的结果是（）

A、3 $\sqrt{2}$ B、2 $\sqrt{3}$ C、2 $\sqrt{2}$ D、2 $\sqrt{6}$

查看试题解析
2. 计算 $\sqrt{8} \times \sqrt{\frac{1}{2}} + {(\sqrt{2})}^{0}$ 的结果为（）

A、 $2 + \sqrt{2}$ B、 $\sqrt{2} + 1$ C、3 D、5

查看试题解析
3. 已知点A、B的坐标分别为（2，5），（﹣4，﹣3），则线段AB的长为（）

A、9 B、10 C、11 D、12

查看试题解析
4. 已知△ABC的边长分别为5，7，8，则△ABC的面积是（）

A、20 B、10 $\sqrt{2}$ C、10 $\sqrt{3}$ D、28

查看试题解析
5. 已知菱形ABCD的面积是120，对角线AC＝24，则菱形ABCD的周长是（）

A、52 B、40 C、39 D、26

查看试题解析
6. 在平面直角坐标系中，一次函数y=kx+b的图象如图所示，则k和b的取值范围是（）

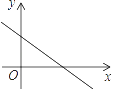A、k＞0，b＞0 B、k＞0，b＜0 C、k＜0，b＞0 D、k＜0，b＜0

查看试题解析
7. 如图，一次函数y₁＝x＋b与一次函数y₂＝kx＋4的图象交于点P（1，3），则关于x的不等式x＋b＞kx＋4的解集是（）

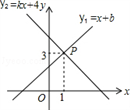A、x＞﹣2 B、x＞0 C、x＞1 D、x＜1

查看试题解析
8. 在平面直角坐标系中，将直线l₁：y=﹣2x﹣2平移后，得到直线l₂：y=﹣2x+4，则下列平移作法正确的是（　　）

A、将l₁向右平移3个单位长度 B、将l₁向右平移6个单位长度 C、将l₁向上平移2个单位长度 D、将l₁向上平移4个单位长度

查看试题解析
9. 济南某中学足球队的18名队员的年龄如下表所示：

年龄/岁

12

13

14

15

人数

3

5

6

4

这18名队员年龄的众数和中位数分别是（）

A、13岁，14岁 B、14岁，14岁 C、14岁，13岁 D、14岁，15岁

查看试题解析
10. 如图，在矩形ABCD中，AD= $\sqrt{2}$ AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：
①∠AED=∠CED；②OE=OD；③BH=HF；④BC﹣CF=2HE；⑤AB=HF，
其中正确的有（）

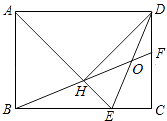A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 2 $\sqrt{\frac{1}{2}}$ ﹣6 $\sqrt{\frac{1}{3}}$ + $\sqrt{8}$ 的结果是.

查看试题解析
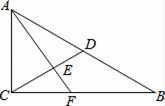
12. 如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，点D在AB上，AD=AC，AF⊥CD交CD于点E，交CB于点F，则CF的长是.

查看试题解析
13. 如图，已知点A的坐标为（5，0），直线y=x+b（b≥0）与y轴交于点B，连接AB，∠α=75°，则b的值为．

查看试题解析
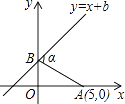14. 有7个数由小到大依次排列，其平均数是38，如果这组数的前4个数的平均数是33，后4个数的平均数是42，则这7个数的中位数是.

查看试题解析
15. 已知直线y＝kx+b与y＝2x+1平行，且经过点（﹣3，4），则函数y＝kx+b的图象可以看作由函数y＝2x+1的图象向上平移个单位长度得到的.

查看试题解析
16. 如图，已知E是正方形ABCD的边AB上一点，点A关于DE的对称点为F，若正方形ABCD的边长为1，且∠BFC＝90°，则AE的长为

查看试题解析
17. 计算：

(1)、 ${(\sqrt{2} + \sqrt{3})}^{2} - \sqrt{24}$ ；

(2)、 $(3 \sqrt{12} - \frac{2}{\sqrt{3}} + \sqrt{48}) \div 2 \sqrt{3}$

查看试题解析
18. 如图，甲、乙两船从港口A同时出发，甲船以30海里/时的速度向北偏东35°的方向航行，乙船以40海里/时的速度向另一方向航行，2小时后，甲船到达C岛，乙船到达B岛，若C，B两岛相距100海里，则乙船航行的方向是南偏东多少度？

查看试题解析
19. 如图，在△ABC中，D，E，F分别是AB，BC，CA的中点，AH是边BC上的高．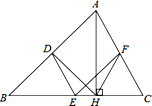

(1)、求证：四边形ADEF是平行四边形；

(2)、求证：∠DHF=∠DEF．

查看试题解析
20. 如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．

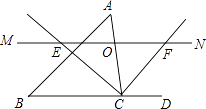(1)、求证：OE=OF；

(2)、若CE=12，CF=5，求OC的长；

(3)、当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．

查看试题解析

21. 某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原始分均为100分.前6名选手的得分如下：

序号项目	1	2	3	4	5	6
笔试成绩/分	85	92	84	90	84	80
面试成绩/分	90	88	86	90	80	85

根据规定，笔试成绩和面试成绩分别按一定的百分比折和成综合成绩（综合成绩的满分仍为100分）

(1)、这6名选手笔试成绩的中位数是分，众数是分.

(2)、现得知1号选手的综合成绩为88分，求笔试成绩和面试成绩各占的百分比.

(3)、求出其余五名选手的综合成绩，并以综合成绩排序确定前两名人选.

查看试题解析

22. 如图，已知菱形ABCD中，∠BAD＝60°，点E、F分别是AB、AD上两个动点，若AE＝DF，连接BF与DE相交于点G，连接CG，与BD相交于H.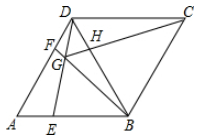

(1)、求∠BGE的大小；

(2)、求证：GC平分∠BGD.

查看试题解析
23. 在一条笔直的公路上有A、B、C三地，C地位于A、B两地之间，甲车从A地沿这条公路匀速驶向C地，乙车从B地沿这条公路匀速驶向A地，在甲车出发至甲车到达C地的过程中，甲、乙两车各自与C地的距离y（公里）与甲车行驶时间（小时）之间的函数关系如图，请根据所给图象关系解答下列问题：

(1)、求甲、乙两车的行驶速度；

(2)、求乙车出发1.5小时后，两车距离多少公里？

(3)、求乙车出发多少小时后，两车相遇？

查看试题解析
24. 如图，已知点A（﹣2，0），点B（6，0），点C在第一象限内，且△OBC为等边三角形，直线BC交y轴于点D，过点A作直线AE⊥BD于点E，交OC于点E

(1)、求直线BD的解析式；

(2)、求线段OF的长；

(3)、求证：BF＝OE.

查看试题解析

年龄/岁	12	13	14	15
人数	3	5	6	4