河南省驻马店市驿城区2018-2019学年八年级下学期数学期末考试试卷

试卷更新日期：2021-04-16 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图形中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若a＞b，则下列结论不一定成立的是（）

A、a-1＞b-1 B、 $\frac{a}{3} > \frac{b}{3}$ C、 $a^{2} > b^{2}$ D、-2a＜-2b

查看试题解析
3. 下列从左到右的变形，是因式分解的是（）

A、2(a﹣b)＝2a﹣2b B、 $a^{2} - b^{2} + 1 = (a - b) (a + b) + 1$ C、 $x^{2} - 2 x + 4 = {(x - 2)}^{2}$ D、 $2 x^{2} - 8 y^{2} = 2 (x - 2 y) (x + 2 y)$

查看试题解析
4. 到三角形三个顶点距离相等的点是（　　）

A、三角形三条边的垂直平分线的交点 B、三角形三条角平分线的交点 C、三角形三条高的交点 D、三角形三条边的中线的交点

查看试题解析
5. 下列条件中，不能判定四边形ABCD是平行四边形的是（）

A、AB∥CD，AD=BC B、AB∥CD，∠B＝∠D C、AB=CD,AD=BC D、AB∥CD，AB＝CD

查看试题解析
6. 一个多边形的内角和比其外角和的2倍多180°，那么这个多边形是（）

A、五边形 B、六边形 C、七边形 D、八边形

查看试题解析
7. 如图，▱ABCD的对角线AC与BD相交于点O，AC⊥BC，且AB＝10，AD＝6，则OB的长度为（）

A、2 $\sqrt{13}$ B、4 C、8 D、4 $\sqrt{13}$

查看试题解析
8. 若解关于x的方程 $\frac{2x - 5}{x - 2} + \frac{m}{2 - x} = 1$ 时产生增根，那么常数m的值为（）

A、4 B、3 C、-4 D、-1

查看试题解析
9. 如图①，在平面直角坐标系中，平行四边形ABCD在第一象限，且AB∥x轴.直线y=-x从原点出发沿x轴正方向平移，在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图②，那么平行四边形ABCD的面积为（）

A、4 B、 $4 \sqrt{2}$ C、 $8 \sqrt{2}$ D、8

查看试题解析

二、填空题

10. 如图，在平行四边形ABCD中，连接AC，按以下步骤作图：分别以点A，C为圆心，以大于 $\frac{1}{2}$ AC的长为半径画弧，两弧分别相交于点M，N，作直线MN交CD于点E，交AB于点F.若AB=5，BC=3，则△ADE的周长为.

查看试题解析
11. 若分式 $\frac{x^{2} - 4}{x + 2}$ 的值为0，则x= ．

查看试题解析
12. 不等式组 ${\begin{matrix} \frac{x - 1}{2} \leq \frac{1}{4} \\ 2 x + 3 < 3 (x + 2) \end{matrix}$ 的最小整数解是.

查看试题解析
13. 如图，在△ABC中，∠B=70°，∠BAC=30°，将△ABC绕点C顺时针旋转得到△EDC，当点B的对应点D恰好落在AC边上时，∠CAE的度数为.

查看试题解析
14. 如图，在Rt△ABC中∠BAC＝90°，D，E分别是AB，BC的中点，F在CA的延长线上∠FDA＝∠B，AC＝6，AB＝8，则四边形AEDF的周长为.

查看试题解析
15. 如图，在Rt△ABC中，∠ACB=90°，∠B=30°，BC=3．点D是BC边上的一动点（不与点B、C重合），过点D作DE⊥BC交AB于点E，将∠B沿直线DE翻折，点B落在射线BC上的点F处．当△AEF为直角三角形时，BD的长为．

查看试题解析

三、解答题

16. 先化简 $\frac{x^{2} + x}{x^{2} - 2 x + 1}$ ÷（ $\frac{2}{x - 1}$ － $\frac{1}{x}$ ），然后再从－2＜x≤2的范围内选取一个合适的x的整数值代入求值

查看试题解析
17. 如图，在△ABC中，AD平分∠BAC，且BD=CD，DE⊥AB于点E，DF⊥AC于点F.

(1)、求证：AB=AC；

(2)、若∠BAC=60°，BC=6，求△ABC的面积.

查看试题解析
18. 如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A（-3，1），B（-1，3），C（0，1）.

（ 1 ）将△ABC以点C为旋转中心旋转180°，画出旋转后的△A₁B₁C；

（ 2 ）平移△ABC，若点A的对应点A₂的坐标为（-5，-3），画出平移后的△A₂B₂C₂；

（ 3 ）若△A₂B₂C₂和△A₁B₁C关于点P中心对称，请直接写出旋转中心P的坐标.

查看试题解析
19. 已知：如图，E、F是▱ABCD的对角线AC上的两点，AF＝CE.

求证：

(1)、△ABE≌△CDF；

(2)、ED∥BF.

查看试题解析
20. 某文具商店的某种毛笔每支售价25元，书法练习本每本售价5元，该商店为促销正在进行优惠活动：
活动1：买一支毛笔送一本书法练习本；

活动2：按购买金额的九折付款.

某学校准备为书法兴趣小组购买这种毛笔20支，书法练习本x（x≥20）本.

(1)、写出两种优惠活动实际付款金额y₁（元），y₂（元）与x（本）之间的函数关系式；

(2)、请问：该校选择哪种优惠活动更合算？

查看试题解析
21. 如图，在四边形ABCD中，AD∥BC，AC与BD交于点E，点E是BD的中点，延长CD到点F，使DF＝CD，连接AF，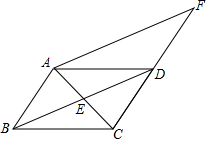

(1)、求证：AE＝CE；

(2)、求证：四边形ABDF是平行四边形；

(3)、若AB＝2，AF＝4，∠F＝30°，则四边形ABCF的面积为．

查看试题解析
22. 倡导健康生活推进全民健身，某社区去年购进A，B两种健身器材若干件，经了解，B种健身器材的单价是A种健身器材的1.5倍，用7200元购买A种健身器材比用5400元购买B种健身器材多10件.

(1)、A，B两种健身器材的单价分别是多少元？

(2)、若今年两种健身器材的单价和去年保持不变，该社区计划再购进A，B两种健身器材共50件，且费用不超过21000元，请问：A种健身器材至少要购买多少件？

查看试题解析
23. 如图，已知等边△ABC，点D在直线BC上，连接AD，作∠ADN=60°，直线DN交射线AB于点E，过点C作CF∥AB交直线DN于点F.

(1)、当点D在线段BC上，∠NDB为锐角时，如图①.
①判断∠1与∠2的大小关系，并说明理由；

②过点F作FM∥BC交射线AB于点M，求证：CF+BE=CD；

(2)、①当点D在线段BC的延长线上，∠NDB为锐角时，如图②，请直接写出线段CF，BE，CD之间的数量关系；
②当点D在线段CB的延长线上，∠NDB为钝角或直角时，如图③，请直接写出线段CF，BE，CD之间的数量关系.

查看试题解析