河南省驻马店市确山县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2021-04-16 类型:期末考试
一、选择题
-
1. 函数 中,自变量x的取值范围是( )A、 B、 C、 D、2. 下列各式计算正确的是( )A、3 ﹣ =3 B、2+ =2 C、 =2 D、 =43. 若正比例函数的图象经过点(2,4),则这个图象也必经过点( )A、(2,1) B、(﹣1,﹣2) C、(1,﹣2) D、(4,2)4. 某中学规定学生的学期体育成绩满分为100,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末考试成绩占50%.小明的三项成绩(百分制)依次是90,80,94,小明这学期的体育成绩是( )A、88 B、89 C、90 D、915. 某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是 =610千克, =608千克,亩产量的方差分别是 =29.6, =2.7. 则关于两种小麦推广种植的合理决策是 ( )A、甲的平均亩产量较高,应推广甲 B、甲、乙的平均亩产量相差不多,均可推广 C、甲的平均亩产量较高,且亩产量比较稳定,应推广甲 D、甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙6. 如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD , B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
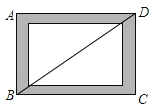 A、四边形ABCD由矩形变为平行四边形 B、BD的长度增大 C、四边形ABCD的面积不变 D、四边形ABCD的周长不变7. 如图,△ABC中,CD是AB边上的高,若AB=1.5,BC=0.9,AC=1.2,则CD的值是( )
A、四边形ABCD由矩形变为平行四边形 B、BD的长度增大 C、四边形ABCD的面积不变 D、四边形ABCD的周长不变7. 如图,△ABC中,CD是AB边上的高,若AB=1.5,BC=0.9,AC=1.2,则CD的值是( ) A、0.72 B、2.0 C、1.125 D、不能确定8. 如图是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=5,BE=12,则EF的长是( )
A、0.72 B、2.0 C、1.125 D、不能确定8. 如图是我国古代著名的“赵爽弦图”的示意图,此图是由四个全等的直角三角形拼接而成,其中AE=5,BE=12,则EF的长是( ) A、7 B、8 C、7 D、79. 如图是甲、乙两个探测气球所在位置的海拔高度 (单位: )关于上升时间 (单位: )的函数图象.有下列结论:
A、7 B、8 C、7 D、79. 如图是甲、乙两个探测气球所在位置的海拔高度 (单位: )关于上升时间 (单位: )的函数图象.有下列结论:①当 时,两个探测气球位于同一高度
②当 时,乙气球位置高;
③当 时,甲气球位置高;
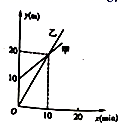
其中,正确结论的个数是( )
A、 个 B、 个 C、 个 D、 个10. 如图,在平面直角坐标系中,四边形ABCD是菱形,点A的坐标为(0, ),分别以A,B为圆心,大于 AB的长为半径作弧,两弧交于点E,F,直线EF恰好经过点D,则点D的坐标为( )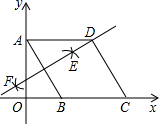 A、(2,2) B、(2, ) C、( ,2) D、( +1,
A、(2,2) B、(2, ) C、( ,2) D、( +1,二、填空题
-
11. 计算: =.12. 学校校园歌手大奖赛共有12位选手入围,按成绩取前6位进入决赛.如果王晓鸥同学知道了自己的成绩,要判断能否进入决赛,用数据分析的观点看,她还需要知道的数据是这12位同学的.13. 若直线y=kx+b与直线y=2x平行,且与y轴相交于点(0,﹣3),则直线的函数表达式是.14. 如图,BD是矩形ABCD的一条对角线,点E、F分别是BD、DC的中点,若AB=8,BC=6,则AE+EF的长为.
 15. 如图,在四边形 中, , 于点 ,动点 从点 出发,沿 的方向运动,到达点 停止,设点 运动的路程为 , 的面积为 ,如果 与 的函数图象如图2所示,那么 边的长度为.
15. 如图,在四边形 中, , 于点 ,动点 从点 出发,沿 的方向运动,到达点 停止,设点 运动的路程为 , 的面积为 ,如果 与 的函数图象如图2所示,那么 边的长度为.
三、解答题
-
16. 计算:(1)、(2)、(2+ )(2- )+ .17. 已知图中的每个方格都是边长为1的小正方形,每个小正方形的顶点称为格点,△ABC的顶点在格点上,称为格点三角形,请按要求完成下列各题(1)、填空:
AB= , BC= , AC=;
(2)、试判断△ABC的形状,并说明理由. 18. 如图,在▱ABCD中,E , F分别是边AB , CD的中点,求证:AF=CE .
18. 如图,在▱ABCD中,E , F分别是边AB , CD的中点,求证:AF=CE . 19. 小梅在浏览某电影评价网站时,搜索了最近关注到的甲、乙、丙三部电影,网站通过对观众的抽样调查,得到这三部电影的评分数据统计图分别如下:
19. 小梅在浏览某电影评价网站时,搜索了最近关注到的甲、乙、丙三部电影,网站通过对观众的抽样调查,得到这三部电影的评分数据统计图分别如下:甲、乙、丙三部电影评分情况统计图




根据以上材料回答下列问题:
(1)、小梅根据所学的统计知识,对以上统计图中的数据进行了分析,并通过计算得到这三部电影抽样调查的样本容量,观众评分的平均数、众数、中位数,请你将下表补充完整:甲、乙、丙三部电影评分情况统计表
电影
样本容量
平均数
众数
中位数
甲
100
3.45
5
乙
3.66
5
丙
100
3
3.5
(2)、根据统计图和统计表中的数据,可以推断其中电影相对比较受欢迎,理由是.(至少从两个不同的角度说明你推断的合理性)
20. 某水果批发市场规定,一次购买苹果不超过100kg(包括100kg),批发价为5元,如果一次购买100kg以上苹果,超过100kg的部分苹果价格打8折.(1)、请填写下表购买量/kg
0
50
100
150
200
…
付款金额/元
0
250
700
…
(2)、写出付款金额关于购买量的函数解析式;(3)、如果某人付款2100元,求其购买苹果的数量.21. 如图,正方形ABCD的对角线AC,BD相交于点O,将BD向两个方向延长,分别至点E和点F,且使BE=DF. (1)、求证:四边形AECF是菱形;(2)、若AC=4,BE=1,直接写出菱形AECF的边长.22. 某学校计划购进A,B两种品牌的足球共50个,其中A品牌足球的价格为100元/个,购买B品牌足球所需费用y(单位:元)与购买数量x(单位:个)之间的关系如图所示
(1)、求证:四边形AECF是菱形;(2)、若AC=4,BE=1,直接写出菱形AECF的边长.22. 某学校计划购进A,B两种品牌的足球共50个,其中A品牌足球的价格为100元/个,购买B品牌足球所需费用y(单位:元)与购买数量x(单位:个)之间的关系如图所示 (1)、请直接写出y与x之间的函数解析式;(2)、若购买B种品牌足球的数量不超过30个,但不少于A种品牌足球的数量,请设计购买方案,使购买总费用W(单位:元)最低,并求出最低费用.23. 如图,在平面直角坐标系中,直线y= x+2与x轴、y轴的交点分别为A、B,直线y=﹣2x+12交x轴于C,两条直线的交点为D;点P是线段DC上的一个动点,过点P作PE⊥x轴,交x轴于点E,连接BP;
(1)、请直接写出y与x之间的函数解析式;(2)、若购买B种品牌足球的数量不超过30个,但不少于A种品牌足球的数量,请设计购买方案,使购买总费用W(单位:元)最低,并求出最低费用.23. 如图,在平面直角坐标系中,直线y= x+2与x轴、y轴的交点分别为A、B,直线y=﹣2x+12交x轴于C,两条直线的交点为D;点P是线段DC上的一个动点,过点P作PE⊥x轴,交x轴于点E,连接BP; (1)、求△DAC的面积;(2)、在线段DC上是否存在一点P,使四边形BOEP为矩形;若存在,写出P点坐标;若不存在,说明理由;(3)、若四边形BOEP的面积为S,设P点的坐标为(x,y),求出S关于x的函数关系式,并写出自变量x的取值范围.
(1)、求△DAC的面积;(2)、在线段DC上是否存在一点P,使四边形BOEP为矩形;若存在,写出P点坐标;若不存在,说明理由;(3)、若四边形BOEP的面积为S,设P点的坐标为(x,y),求出S关于x的函数关系式,并写出自变量x的取值范围.