河南省周口市川汇区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2021-04-16 类型:期末考试
一、选择题
-
1. 代数式 在实数范围内有意义,则a的取值范围是( )A、 B、 C、 D、2. 《九章算术》中的“折竹抵地”问题:一根竹子高1丈(1丈 尺),折断后竹子顶端落在离竹子底端6尺处,折断处离地面的高度是多少?( )A、3.2 B、4.2 C、5 D、83. 以三角形三边中点和三角形三个顶点能画出平行四边形有( )个.A、1 B、2 C、3 D、44. 已知函数 ,不在该函数图象上的点是( )A、(3,4) B、(4,-3) C、(4,3) D、(-3,4)5. 若正比例函数y=mx(m是常数,m≠0)的图象经过点A(m,4),且y的值随x值的增大而减小,则m等于( )A、2 B、﹣2 C、4 D、﹣46. 平移直线 得到直线 ,正确的平移方式是( )A、向上平移5个单位长度 B、向下平移5个单位长度 C、向左平移6个单位长度 D、向右平移6个单位长度7. 某校规定学生的学期数学成绩满分为100分,其中研究性学习成绩占40%,期末卷面成绩占60%,小明的两项成绩(百分制)依次是80分,90分,则小明这学期的数学成绩是( )A、80分 B、82分 C、84分 D、86分8. 据统计,某住宅楼30户居民五月份最后一周每天实行垃圾分类的户数依次是:27,30,29,25,26,28,29,那么这组数据的中位数和众数分别是( )A、25和30 B、25和29 C、28和30 D、28和299. 已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为矩形的是( )A、∠A=∠B B、∠A=∠C C、AC=BD D、AB⊥BC10. 如图①,点E从菱形ABCD的顶点 出发,沿 以 的速度匀速运动到点D.图②是点E运动时, 的面积y( )随着时间x(s)变化的关系图象,则菱形的边长为( )
 A、3 B、4 C、 D、5
A、3 B、4 C、 D、5二、填空题
-
11. 计算: .12. 在等腰 中, , ,则底边上的高等于.13. 两个面积都为8的正方形纸片,其中一个正方形的顶点与另一个正方形对角线的交点重合,则两个正方形纸片重叠部分的面积为.14. 已知一次函数 的图象经过点 ,则不等式 的解是.15. 如图,直线 与x轴正半轴交于点A,与y轴交于点B,将 沿 翻折,使点O落在点C处,点D是线段AB的中点,射线OD交线段AC于点E,若 为直角三角形,则k的值为.

三、解答题
-
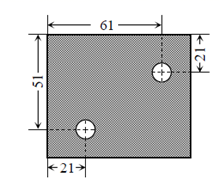
16. 计算题:(1)、 ;(2)、已知 , ,求代数式 的值.17. 如图,已知带孔的长方形零件尺寸(单位:mm),求两孔中心的距离.
 18. 如图,在 中, , ,垂足分别为 .求证四边形AFCE是矩形.
18. 如图,在 中, , ,垂足分别为 .求证四边形AFCE是矩形.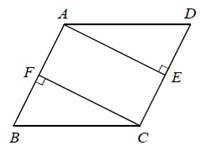 19. 如图,在平面直角坐标系中,直线 与坐标轴交于A、B,过线段AB的中点M作AB的垂线,交x轴于点C.
19. 如图,在平面直角坐标系中,直线 与坐标轴交于A、B,过线段AB的中点M作AB的垂线,交x轴于点C.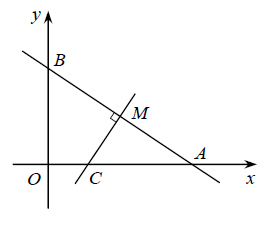 (1)、填空:线段OB,OC,AC的数量关系是;(2)、求直线CM的解析式.20. 下图是交警在一个路口统计的某个时段来往车辆的车速情况.应用你所学的统计知识,写一份简短的报告,让交警知道这个时段路口来往车辆的车速情况.
(1)、填空:线段OB,OC,AC的数量关系是;(2)、求直线CM的解析式.20. 下图是交警在一个路口统计的某个时段来往车辆的车速情况.应用你所学的统计知识,写一份简短的报告,让交警知道这个时段路口来往车辆的车速情况. 21. 甲、乙两台机床同时生产一种零件.在连续 周中,两台机床每周出次品的数量如下表.
21. 甲、乙两台机床同时生产一种零件.在连续 周中,两台机床每周出次品的数量如下表.甲
乙
(1)、分别计算两组数据的平均数与方差;(2)、两台机床出次品的平均数怎样?哪台机床出次品的波动性小?22. 某学校计划在总费用2300元的限额内,租用汽车送234名学生和6名教师集体外出活动,每辆车上至少要有1名教师.现有甲乙两种大客车,它们的载客量和租金如下表所示.甲种客车
乙种客车
载客量/(人/量)
45
30
租金/(元/辆)
400
280
(1)、填空:要保证师生都有车坐,汽车总数不能小于;若要每辆车上至少有1名教师,汽车总数不能大于.综合起来可知汽车总数为.(2)、请给出最节省费用的租车方案.23. 在平面直角坐标系 中,已知直线 与x轴交于点A,与y轴交于点B,点C为OB的中点,点D是线段AB上的动点,四边形OEDC是平行四边形,连接EA.设点D横坐标为m.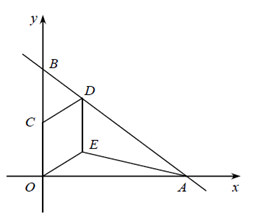 (1)、填空:①当 时, 是矩形;②当 时, 是菱形;(2)、当 的面积为9时,求点D的坐标.
(1)、填空:①当 时, 是矩形;②当 时, 是菱形;(2)、当 的面积为9时,求点D的坐标.