河南省益阳市赫山区2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2021-04-16 类型:期末考试
一、选择题
-
1. 如图,在△ABC中,∠C=90°,∠A=30°,AB=6,则BC=( )
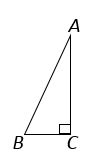 A、3 B、 C、 D、62. 如图,OC为∠AOB的平分线,CM⊥OB于M,OC=5,OM=4,则点C到射线OA的距离为( )
A、3 B、 C、 D、62. 如图,OC为∠AOB的平分线,CM⊥OB于M,OC=5,OM=4,则点C到射线OA的距离为( ) A、2 B、3 C、4 D、53. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A、2 B、3 C、4 D、53. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A、7.5平方千米 B、15平方千米 C、75平方千米 D、750平方千米4. 若正多边形的一个外角是 ,则该正多边形的内角和为( )A、 B、 C、 D、5. 菱形不具备的性质是( )A、四条边都相等 B、对角线一定相等 C、是轴对称图形 D、是中心对称图形6. 已知平行四边形ABCD,下列条件中,不能判定这个平行四边形为菱形的是( )A、AB=CD B、AB=BC C、AC平分∠BAD D、AC⊥BD7. 某班组织了针对全班同学关于“你最喜欢的一项体育活动”的问卷调查后,绘制出频数分布直方图,由图可知,下列结论正确的是( )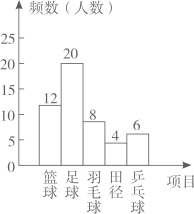 A、最喜欢篮球的人数最多 B、最喜欢羽毛球的人数是最喜欢乒乓球人数的两倍 C、全班共有50名学生 D、最喜欢田径的人数占总人数的10%8. 在平面直角坐标系的第二象限内有一点 ,点 到 轴的距离为3,到 轴的距离为4,则点 的坐标是( )A、 B、 C、 D、9. 若一次函数 的函数值 随 的增大而增大,则( )A、 B、 C、 D、10. 如图,点P是边长为2的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则 的最小值是( )
A、最喜欢篮球的人数最多 B、最喜欢羽毛球的人数是最喜欢乒乓球人数的两倍 C、全班共有50名学生 D、最喜欢田径的人数占总人数的10%8. 在平面直角坐标系的第二象限内有一点 ,点 到 轴的距离为3,到 轴的距离为4,则点 的坐标是( )A、 B、 C、 D、9. 若一次函数 的函数值 随 的增大而增大,则( )A、 B、 C、 D、10. 如图,点P是边长为2的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则 的最小值是( )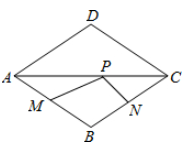 A、1 B、2 C、 D、4
A、1 B、2 C、 D、4二、填空题
-
11. 在平面直角坐标系中,将点(3,﹣2)先向右平移2个单位长度,再向上平移3个单位长度,则所得点的坐标是.12. 函数 中,自变量X的取值范围是.13. 某校对初一全体学生进行一次视力普查,得到如下统计表,视力在 这个范围的频率为.
视力x
频数
4.0≤x<4.3
20
4.3≤x<4.6
40
4.6≤x<4.9
70
4.9≤x<5.2
60
5.2≤x<5.5
10
14. 阅读后填空:已知:如图, , , 、 相交于点 .
求证: .
分析:要证 ,可先证 ;
要证 ,可先证 ;
而用可证 (填 或 或 ).
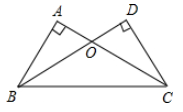 15. 如图,矩形ABCD的对角线AC与BD相交点O , ,P、Q分别为AO、AD的中点,则PQ的长度为 .
15. 如图,矩形ABCD的对角线AC与BD相交点O , ,P、Q分别为AO、AD的中点,则PQ的长度为 . 16. 以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是 .17. 如图,直线 经过点 ,则关于 的不等式 的解集是.
16. 以正方形ABCD的边AD作等边△ADE,则∠BEC的度数是 .17. 如图,直线 经过点 ,则关于 的不等式 的解集是.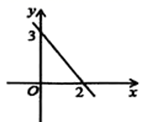 18. 如图,在正方形 中, 是 边上的点,过点 作 于 ,若 ,则 的度数为.
18. 如图,在正方形 中, 是 边上的点,过点 作 于 ,若 ,则 的度数为. 19. 如图,在 中, , 为 边上的高, 为 边上的中线, , ,求 的长.
19. 如图,在 中, , 为 边上的高, 为 边上的中线, , ,求 的长.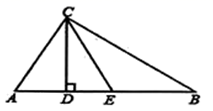 20. 如图,在 中, 于 , 于 ,连接 , .求证:四边形 是平行四边形.
20. 如图,在 中, 于 , 于 ,连接 , .求证:四边形 是平行四边形.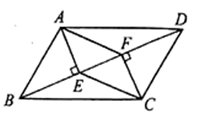 21. 小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示.
21. 小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示. (1)、根据函数的定义,请判断变量h是否为关于t的函数?(2)、结合图象回答:
(1)、根据函数的定义,请判断变量h是否为关于t的函数?(2)、结合图象回答:①当 时,h的值大约是多少?并说明它的实际意义.
②秋千摆动第二个来回需多少时间?
22. 已知 与x成正比例,且 时, .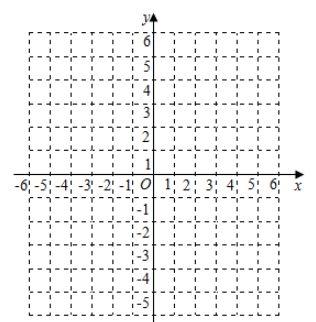 (1)、求y关于x的函数表达式;(2)、在图中画出(1)中所求函效的图象并求出图象与两坐标轴围成的图形的面积.23. 为了解某校八年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位: )绘制成不完整的频数分布表和频数分布直方图.
(1)、求y关于x的函数表达式;(2)、在图中画出(1)中所求函效的图象并求出图象与两坐标轴围成的图形的面积.23. 为了解某校八年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位: )绘制成不完整的频数分布表和频数分布直方图.学生立定路远测试成绩的频数分布表
分组
频数
12
10
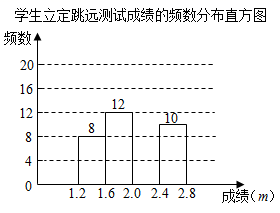
请根据图表中所提供的信息,完成下列问题:(1)、求表中 , 的值;(2)、请把频数分布直方图补充完整;(3)、该校八年级共有800名学生,估计该年级学生立定跳远成绩在 范围内的学生有多少人?24. 先将一矩形 置于直角坐标系中,使点 与坐标系的原点重合,边 , 分别落在 轴、 轴上(如图1),再将此矩形在坐标平面内按逆时针方向绕原点旋转 (如图2),若 , ,求图1和图2中点 的坐标.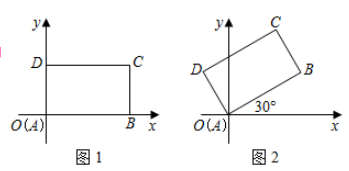 25. 如图,在菱形 中,对角线 与 交于点 .过点 作 的平行线,过点 作 的平行线,两直线相交于点 .
25. 如图,在菱形 中,对角线 与 交于点 .过点 作 的平行线,过点 作 的平行线,两直线相交于点 .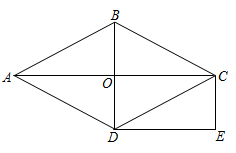 (1)、求证:四边形 是矩形;(2)、若 , ,求菱形 的面积.26. 一辆汽车在某次行驶过程中,油箱中的剩余油量 (升)与行驶路程 (千米)之间是一次函数关系,其部分图象如图所示.
(1)、求证:四边形 是矩形;(2)、若 , ,求菱形 的面积.26. 一辆汽车在某次行驶过程中,油箱中的剩余油量 (升)与行驶路程 (千米)之间是一次函数关系,其部分图象如图所示.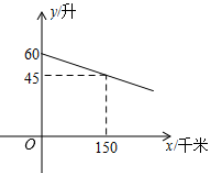 (1)、求 关于 的函数关系式;(不需要写自变量 的取值范围)(2)、已知当油箱中的剩余油量为10升时,该汽车会开始提示加油,在此次行驶过程中,行驶了482千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?
(1)、求 关于 的函数关系式;(不需要写自变量 的取值范围)(2)、已知当油箱中的剩余油量为10升时,该汽车会开始提示加油,在此次行驶过程中,行驶了482千米时,司机发现离前方最近的加油站有30千米的路程,在开往该加油站的途中,汽车开始提示加油,这时离加油站的路程是多少千米?