河南省信阳市固始县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2021-04-16 类型:期末考试
一、选择题
-
1. 下列各式一定是二次根式的是( )A、 B、 C、 D、2. 使式子 成立的x的取值范围是( )A、x≥﹣2 B、x>﹣2 C、x>﹣2,且x≠2 D、x≥﹣2,且x≠23. 如图所示,圆柱的高AB=3,底面直径BC=3,现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食,则它爬行的最短距离是( )
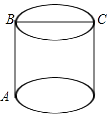 A、 B、 C、 D、4. 如图所示,有一块直角三角形纸片,∠C=90°,AC=8cm,BC=6cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )
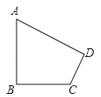
A、 B、 C、 D、4. 如图所示,有一块直角三角形纸片,∠C=90°,AC=8cm,BC=6cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为( )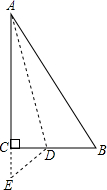 A、1cm B、2cm C、3cm D、4cm5. 如图,在菱形纸片ABCD中,∠A=60°,点E在BC边上,将菱形纸片ABCD沿DE折叠,点C落在AB边的垂直平分线上的点C′处,则∠DEC的大小为( )
A、1cm B、2cm C、3cm D、4cm5. 如图,在菱形纸片ABCD中,∠A=60°,点E在BC边上,将菱形纸片ABCD沿DE折叠,点C落在AB边的垂直平分线上的点C′处,则∠DEC的大小为( ) A、30° B、45° C、60° D、75°6. 如图,在Rt△ABC中,∠B=90°,BC=3,AB=4,点D,E分别是AB,AC的中点,CF平分Rt△ABC的一个外角∠ACM,交DE的延长线于点F,则DF的长为( )
A、30° B、45° C、60° D、75°6. 如图,在Rt△ABC中,∠B=90°,BC=3,AB=4,点D,E分别是AB,AC的中点,CF平分Rt△ABC的一个外角∠ACM,交DE的延长线于点F,则DF的长为( ) A、4 B、5 C、5.5 D、67. 下列各曲线中表示y是x的函数的是( )A、
A、4 B、5 C、5.5 D、67. 下列各曲线中表示y是x的函数的是( )A、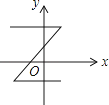 B、
B、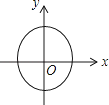 C、
C、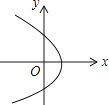 D、
D、 8. 如图,直线y=ax+b过点A(0,2)和点B(﹣3,0),则方程ax+b=0的解是( )
8. 如图,直线y=ax+b过点A(0,2)和点B(﹣3,0),则方程ax+b=0的解是( )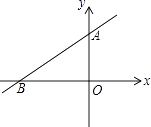 A、x=2 B、x=0 C、x=﹣1 D、x=﹣39. 在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数10. 若一组数据a1 , a2 , a3的平均数为4,方差为3,那么数据a1+2,a2+2,a3+2的平均数和方差分别是( )A、4,3 B、6,3 C、3,4 D、6,5
A、x=2 B、x=0 C、x=﹣1 D、x=﹣39. 在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数10. 若一组数据a1 , a2 , a3的平均数为4,方差为3,那么数据a1+2,a2+2,a3+2的平均数和方差分别是( )A、4,3 B、6,3 C、3,4 D、6,5二、填空题
-
11. 若实数x , y满足 + =0,则以x , y的值为边长的等腰三角形的周长为 .
12. 学校操场边上一块空地(阴影部分)需要绿化,测出CD=6m,AD=8m,BC=24m,AB=26m,AD⊥CD,那么需要绿化部分的面积为. 13. 如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是 .
13. 如图,在平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,则平行四边形ABCD的周长是 . 14. 若函数y=(a+3)x+a2﹣9是正比例函数,则a= .15. 有一组数据:2,5,5,6,7,这组数据的平均数为.
14. 若函数y=(a+3)x+a2﹣9是正比例函数,则a= .15. 有一组数据:2,5,5,6,7,这组数据的平均数为.三、解答题
-
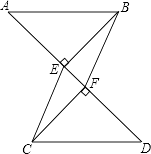
16. 求值(1)、(2)、 |17. 一阵大风把一根高为9m的树在离地4m处折断,折断处仍相连,此时在离树3.9m处,一头高1m的小马正在吃草,小马有危险吗?为什么?18. 已知直线l1:y= x-3与x轴,y轴分别交于点A和点B.(1)、求点A和点B的坐标;(2)、将直线l1向上平移6个单位后得到直线l2 , 求直线l2的函数解析式;(3)、设直线l2与x轴的交点为M,则△MAB的面积是 .19. 如图,已知:AB∥CD,BE⊥AD,垂足为点E,CF⊥AD,垂足为点F,并且AE=DF.
求证:四边形BECF是平行四边形.
 20. 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离 y (千米)与 x (时间)之间的函数关系图象.
20. 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑摩托车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离 y (千米)与 x (时间)之间的函数关系图象.
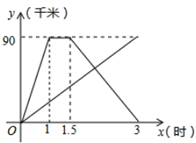 (1)、求甲从B地返回A地的过程中, y 与 x 之间的函数关系式,并写出自变量
(1)、求甲从B地返回A地的过程中, y 与 x 之间的函数关系式,并写出自变量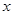 的取值范围; (2)、若乙出发后2小时和甲相遇,求乙从A地到B地用了多长时间?21. 如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,连接CG.
的取值范围; (2)、若乙出发后2小时和甲相遇,求乙从A地到B地用了多长时间?21. 如图,在正方形ABCD中,E、F分别是边AB、BC的中点,连接AF、DE相交于点G,连接CG. (1)、求证:AF⊥DE;(2)、求证:CG=CD.
(1)、求证:AF⊥DE;(2)、求证:CG=CD.